Applications Of Diagonal Matrix In Computer Science
Examples of matrix operations. Thats the study of matrices especially identity matrices under linear.

Matrix Diagonalization Examples 2x2 Non Diagonalizable 3x3 Diagonalizable With Repeated Eigenvalue Youtube
Resent linear transformations that is generalizations of linear functions such as f x 2x.

Applications of diagonal matrix in computer science. Many applications of matrices in both engineering and science utilize eigenvalues and sometimes eigenvectors. This special structure appears often in scientific computing and computer graphics 1 2. Reduce the dimensions of the matrices based on the importance of the topics.
In order to guide the students to know the application of matrix in the computer science and technology to stimulate interest in learning. A major application of matrices is to rep- algorithms that create Google page rankings. The graphic software uses the matrix to perform the linear transformations into the images.
LINEAR ALGEBRA AND ITS APPLICATIONS I Almost Diagonal Matrices with Multiple or Close Eigenvalues J. Conclusion There are so many application of Linear Algebra in Computer Science. Matrices are also used for encryptiondecryption of codes or messages.
A tridiagonal matrix has nonzero elements only on the main diagonal the diagonal upon the main diagonal and the diagonal below the main diagonal. In PCA essentially we diagonalize the covariance matrix of X by eigenvalue decomposition since the covariance matrix is symmetric- C VLVᵀ In Python- from numpy import cov from numpylinalg import eig X array-2 -2 0 0 2 2 C covX To do eigendecomposition of C values vectors eigC Project data into pricipal directions P vectorsTdotXT printPT Output-. From simple circuit solving to large web engine algorithms.
Secondary diagonal matrix i n - i - 1. Principal diagonal matrix i i. The row-column condition is row numberOfRows - column - 1.
In general the inverse of a tridiagonal matrix is a semiseparable matrix and vice versa. Application of matrix in the field of computer is too muchIt is a simple calculation tool can be represented in a simple form and complex form. Condition for Secondary Diagonal.
WILKINSON National Physical Laboratory Teddington England 1. Routinely with the aid of computer graphics. Each coordinate of the input vector simply gets multiplied by the corresponding diagonal element and there are no cross-term between different coordinates.
Document-Topic matrix Topic Importance Diagonal Matrix and Topic-term matrix. This paper gives several examples about computer science and technology to answer by using matrix method. Findings Matrices are used for making Graphics and for Creating and modifying Images.
Closed form solutions can be computed for special cases such as symmetric matrices with all diagonal and off-diagonal elements equal or Toeplitz matrices and for the general case as well. The rows and columns in the matrix represent rows and columns of the pixels. The numerical values represent the pixel colour value.
The Images formed can be further transformed or mutated by changing these co ordinates. Many of the applications involve the use of eigenvalues and eigenvectors in the process of trans-. In this method we use one loop ie.
Because many of them require real-time execution the solver must compute the result quickly as well as correctly. Any matrix can be multiplied element- motion on a two-dimensional computer screen and also in the calculation of wise by a scalar from its associated field. It helps to project the 3D images in the two-dimensional plane.
The heart beat of computer science is in linear algebra especially in the generation and formation of computer coding schemes. Solution of linear system. Control theory vibration analysis electric circuits advanced dynamics and quantum mechanics are just a few of the application areas.
These smaller matrices are then used to match words to the topic and create a distribution of words and topics. Use SVD to break the text matrix into three sub-matrices. In video gaming industry matrices are major mathematic tools to construct and manipulate a realistic animation of a polygonal figure.
Where 0. One important application of this is if you have a vector differential equation X t A X t B. Below is the implementation of the above approach.
A loop to find the diagonal elements as per the below formula. Images are a collection of points in this case matrix co ordinates are used to represent these points. INTRODUCTION In a number of algorithms for finding eigenvalues of a matrix Al the latter is reduced by an iterative sequence of similarity transformations to almost diagonal form.
Video gaming industry maybe the earliest industry to rely heavily on computer graphics is now representing rendered polygon in 3-Dimensions.

How To Calculate The Inverse Of A Diagonal Matrix Quora

Types Of Matrices Definition Differences Video Lesson Transcript Study Com

Print Matrix In Diagonal Pattern Geeksforgeeks

What Is Diagonal Matrix Definition Of A Diagonal Matrix Is Zero Matrix Is Diagonal Matrix Youtube

Diagonal Matrix An Overview Sciencedirect Topics

Center Element Of Matrix Equals Sums Of Half Diagonals Geeksforgeeks

Program To Interchange Diagonals Of Matrix Geeksforgeeks

Types Of Matrices Types Of Matrices Solved Examples

Diagonal Matrix An Overview Sciencedirect Topics

Diagonal Matrix Definition Examples And Its Properties

Diagonal Matrix An Overview Sciencedirect Topics

Sum Of All Parts Of A Square Matrix Divided By Its Diagonals Geeksforgeeks

Diagonal Matrix An Overview Sciencedirect Topics

Matrices Matrices A Matrix Is A Rectangular Array

Diagonal Matrix An Overview Sciencedirect Topics

Diagonal Matrix An Overview Sciencedirect Topics

Matrices Matrices A Matrix Is A Rectangular Array
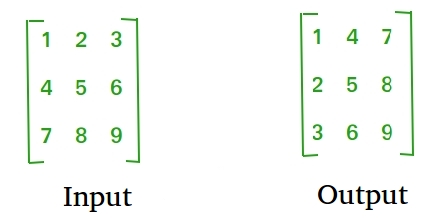
Python Program To Find Transpose Of A Matrix Geeksforgeeks