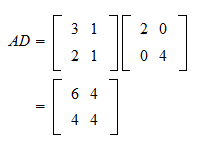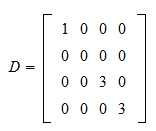Diagonal Matrix Multiplication Rules
TheproductABisdefined to be thempmatrixC cij such that. Since detE 1 for a combination rule detE 1 for a swap ruleand detE cfor a multiply rule with multiplierc6 0 it follows thatfor any elementary matrixEthere is the determinant multiplication rule detEA detE detA.
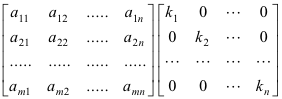
Effect Of Multiplying A Matrix By A Diagonal Matrix
Proposition Let be a matrix and a diagonal matrix.
Diagonal matrix multiplication rules. In the theory of Lie groups the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group. In mathematics a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices. From this one can deduce that a square matrix A is invertible if and only if A T is invertible and in this case we have A 1 T A T 1By induction this result extends to the general case of multiple matrices where we find.
LetA aik be anmnmatrix and bkj be annpmatrix. The transpose respects addition. Matrix multiplication The product of matrices AandBis defined if thenumber of columns inAmatches the number ofrows inB.
Ie AT ij A ji ij. Therefore the determinant must be 0. Note that the order of the factors reverses.
D D T. In Mathematics one matrix by another matrix. P Q.
The effect is that of multiplying the i-th row of matrix A by the factor k i ie. This is because of property 2 the exchange rule. IfEis an elementary matrix for a multiply rule withmultiplierc6 0 thendetEA cdetA.
Intuitively a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines which break it up or partition it into a collection of smaller matrices. The successive rows of the original matrix are simply multiplied by successive diagonal elements of the diagonal matrix. To multiply a matrix by another matrix we need to follow the rule DOT PRODUCT.
Same order diagonal matrices gives a diagonal matrix only after addition or multiplication. In mathematics the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential functionIt is used to solve systems of linear differential equations. If two rows of a matrix are equal its determinant is zero.
Let X be an nn real or complex matrix. On the one hand exchanging the two identical rows does not change the determinant. Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A.
Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. The operation of taking the transpose is an involution self-inverse. When we multiply a matrix by a scalar value then the process is known as scalar multiplication.
Multiplication by a diagonal matrix Two useful results about products involving diagonal matrices are reported below. What is the effect of post-multiplying a matrix by a diagonal matrix A. Lets learn about the properties of the diagonal matrix now.
Transpose of the diagonal matrix D is as the same matrix. By a diagonal matrix A. Then the product is a matrix whose -th row is equal to the -th row of multiplied by for every.
I then discussed block diagonal matrices ie block matrices in which the off-diagonal submatrices are zero and in a multipart series of posts showed that we can uniquely and maximally partition any square matrix into block. On the other hand exchanging the two rows changes the sign of the determinant. In a previous post I discussed the general problem of multiplying block matrices ie matrices partitioned into multiple submatrices.
Let us discuss how to multiply a matrix by another matrix its algorithm formula 22 and 33 matrix multiplication. P Q.

Ppt Review On Linear Algebra Powerpoint Presentation Free Download Id 2382567

1 7 Diagonal Triangular And Symmetric Matrices Ppt Download

Block Diagonal Matrices Youtube

Finding Determinant Of Matrix Through Row Operations Problem Help Mathematics Stack Exchange

6 2 4 Transforming A Matrix To An Upper Triangular Matrix Youtube

Diagonal Matrix Definition Examples And Its Properties

Diagonal Matrix An Overview Sciencedirect Topics

1 7 Diagonal Triangular And Symmetric Matrices Ppt Download
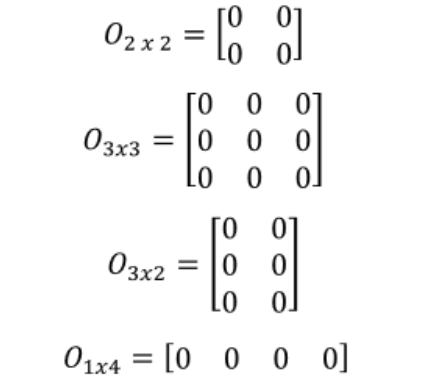
Definition Of A Zero Matrix Studypug
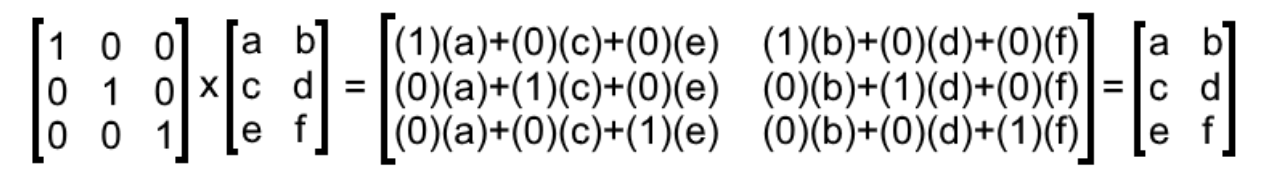
What Is An Identity Matrix Studypug
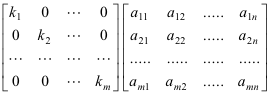
Effect Of Multiplying A Matrix By A Diagonal Matrix

7 1 Matrices Vectors Addition And Scalar Multiplication
For A Symmetric Matrix With Different Diagonal Elements Is There A Shortcut Method Other Than The Conventional One To Find Its Determinant Quora