Multiplying Quaternion Example
Every quaternion has a polar decomposition. There is no real number c to satisfy c210.
Maths Quaternions Martin Baker Math Math Formulas Algebra
The rotation operator becomes where v represents the object to rotate specified in quaternion form.
Multiplying quaternion example. Enter the scalar q 4 and i j and k components q 1 q 2 q 3 of quaternion two. Quaternion multiplication is defined as Equation 224. To define the product of quaternions in yet another way.
These quaternions can be expressed in ijk notation as shown. Quaternion works the same way as matrix. I j and k which are imaginary numbers.
The same sort of things is going on with the cross product of two vectors and quaternion multiplication. 7459 q2. The solution is quaternion introduced by Hamilton in 1843 it defined three fundamental quaternion units.
A 0i 0j 0j for a2R. Puzzle Check that this formula gives the same result for quaternion multiplication as the explicit rules for multiplying i j and k. Such quaternions will be denoted simply by aso 3 denotes 3 0i 0j 0ksimilarly to how 3 2C denotes 3 0 i.
Quaternion addition is simply the four-tuple addition of quaternion representations s 1 v 1 s 2 v 2 s 1 s 2 v 1 v 2. They are subscripted with 0 1 2 and 3 which correspond to the X Y Z and W components respectively. Given orientation A and orientation B you can calculate rotation R that would transform object from A to B by multiplying B with inverse of A.
For example if you have two or more orientations represented as matrices it. Assume you have two quaternions q and p. This example shows how to determine the product of 1-by-4 with two 1-by-4 quaternions.
And he denoted this 4D complex number set as Quaternion. R 1 05 05 075. Orientation is rotation from identity transform and delta is rotation from one transform to the next.
Our rule crazy looking rule 1 is just the rule for complex multiplication. The Quaternion Multiplication q q1 q2 calculator computes the resulting quaternion q from the product of two q1 and q2. The product of a quaternion with its reciprocal should equal 1 and the.
So ah h a ahfor a2R. For example if Q L represents the linear operator of multiplication on the left by quaternion q and P R represents the linear operator of multiplication on the right by quaternion p the above identity reads. Mult quatmultiply q r mult 24 05000 12500 15000 02500 19000 11000 21000 -09000.
For instance if q e θ 1 n 1 and r e θ 2 n 2 then q r would represent a composition of rotations. Enter the scalar q 4 and i j and k components q 1 q 2 q 3 of quaternion one q1 separated by commas eg. Theyre numerically the same.
Multiplying two unit quaternions has the effect of rotating around one axis and then another. It works like three vectors in 3D space. So assuming your quaternions represent w1 xi yj zk multiplication would be something like quaternion operatorquaternion a quaternion b return aw bw - ax bx - ay by - az bz 1 aw bx ax bw ay bz - az by i aw by - ax bz ay bw az bx j aw bz ax by - ay bx az bw k.
Later Hamilton realized 4 dimensional complex numbers are required for multiplication to be closed by adding an additional imaginary part k. Notice that quaternion multiplication is associative q 1 q 2q 3 q 1 q 2 q 3 but is not commutative q 1 q 2 q 2 q 1. The equation c210 gives the contradiction.
It is often convenient to employ other notations for quaternion multiplication in which this property is not so obvious. Quaternions can be added as vectors and we de ne a distributive multiplication on H. A unit quaternion is a quaternion of norm one.
3 Geometry of Complex Numbers The set of complex numbers is denoted by Cand as a reminder C fxiyjxy 2 Rg. 2 1 01 01. To multiply these two quaternions together distribute the components of p to the components of q.
First rotate your vector by θ 1 around the axis n 1 and then rotate your vector by θ 2 around the axis n 2. For example 1i2i 1 i21 ii 22ii1 3i. Distributing the real component is simple.
The muliplication of two quaternion units works like cross products with two vectors. Quaternions simplify the calculations required when compositing rotations. Q 1 0 1 0.
To compose a sequence of frame rotations multiply the quaternions in the order of the desired sequence of rotations. Determine the Product of Two Different Quaternions. For example i times j equals to k and j times i equals to minus k.
We de ne multiplication by a2R on either the left or the right to be scalar multiplication. For example to apply a p quaternion followed by a q quaternion multiply in the order pq. V0vw0w v0w0 vw.
Using conjugation and the norm makes it possible to define the reciprocal of a non-zero quaternion. Dividing a non-zero quaternion q by its norm produces a unit quaternion Uq called the versor of q.
Quaternion Multiplication I 2 J 2 K 2 Ijk 1 And Octonion Download Scientific Diagram
Multiplying Complex Numbers Youtube
Humane Rigging Chapter 03 Video 03 Math Video Neon Signs
Pin On Maya
Quaternion
Pin On Abstract Algebra Videos
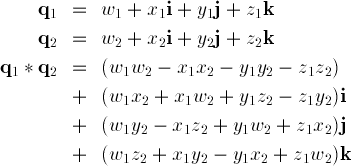
Cs184 Using Quaternions To Represent Rotation
Quaternion Second Life Wiki
Visualizing Quaternions 4d Numbers With Stereographic Projection Youtube
Multiplication Of Quaternions Programmer Sought
Pin On Math Day 1
Quaternions
Immersive Linear Algebra Algebra Basic Math Math
Quaternion Second Life Wiki
Pin On Algebra
Quaternions As 4x4 Matrices Connections To Linear Algebra Youtube Algebra Equations Algebra Math Formulas
Quaternion Multiplication I 2 J 2 K 2 I J K 1 And Octonion Download Scientific Diagram
Unit Quaternion Description Of Spatial Rotation In 3d Electron Cryo Microscopy Biorxiv
Pin On Matrices Math
