Are Skew Symmetric Matrices Invertible
7 Problems and Solutions on skew-symmetric Hermitian symmetric matrices. Answer verified by Toppr Upvote 0.

Proof If N Is Odd Then Det A 0 For Skew Symmetric Matrix Youtube
As such any matrix whose multiplication takes place from the right or the left with the matrix in question results in the.
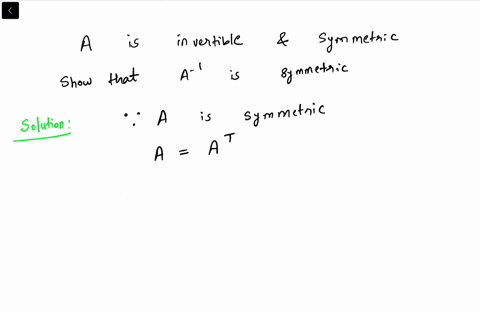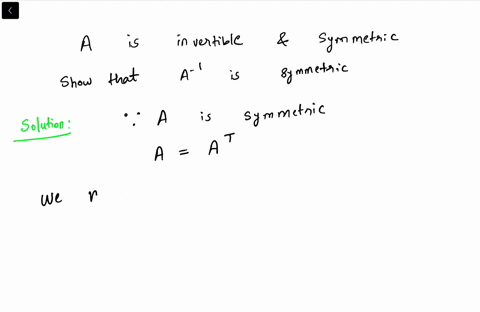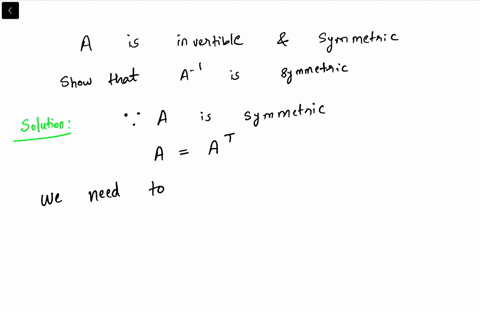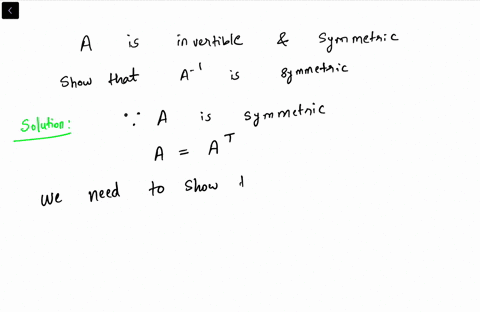
Are skew symmetric matrices invertible. No the diagonal being zero does not mean the matrix must be non-invertible. I Let A be a diagonalizable n x n-matrix of eigenvalues - 1 and 1. Iii Let C be an n x n-matrix such that C2 -.
Determinant of Skew Symmetric Matrix. A symmetric matrix may not by invertible. Therefore for a matrix to be skew symmetric A-A.
Hence their inverse does not exist. If it exists is. The symmetric matrix should be a square matrix.
The inverse of a skew symmetric matrix. If we consider the zero square matrix of any dimension for a moment then we can clearly see its equal to its own transpose. What is meant by the inverse of a symmetric matrix.
The question you should be asking is if all symmetric matrices are invertible. The diagonal of a skew-symmetric matrix is always 0 does not mean that its determinant be 0. A-1T AT-1A-1 as A is symmetric.
Recall that a symmetric matrix is such that it is equal to its own transpose. 8 Symmetric and skew symmetric matrices symmetric A matrix M is called symmetric if it is equal to its transpose that is M -M. Let H H nn be an invertible φ-hermit an matrix.
Ii Let B be a skew-symmetric n x n-matrix where n is odd. Skew symmetric A matrix M is called skew symmetric if it is equal to its transpose that is M -M. The transpose of a symmetrizable matrix is symmetrizable since A T D S T S D D 1 D S D displaystyle Amathrm T DSmathrm T SDD-1DSD and D S D displaystyle DSD is symmetric.
A square matrix Ais called Skew-symmetric if AT-A that is Aij-Ajifor every iand j. Theorem a If Ais invertible and skew-symmetric then the inverse of Ais skew-symmetric. This matrix is skew-symmetric with determinant 1.
The inverse of a skew symmetric matrix of odd order is 1a symmetric matrix 2a skew symmetric matrix 3a diagonal matrix 4does not exist. Look at following example. Find the determinant of the following matrices by using properties of determinants and decide with reasons if they are invertible or not.
Since the main diagonal elements are reflected into themselves all of the main diagonal elements of a skew-symmetric matrix must be zeroes aii aii only if aii 0. Prove that if two H φ-symmetric matrices A and A. Show that A is an invertible matrix whose inverse is A-1 A.
A 3 6 1 0 4 2 0 0 2 A b 2 1. The eigenvalue of the symmetric matrix should be a real number. The inverse of a skew symmetric matrix if it exists is.
When identity matrix is added to skew symmetric matrix then the resultant matrix is invertible. 2x2 matrix with all entries 1 is symmetric but not invertible. Since A as a skew-symmetric matrix does not have real eigenvalues other than possibly zero M-I is invertible for anotin S.
The short answer is no. An matrix is said to be symmetrizable if there exists an invertible diagonal matrix and symmetric matrix such that. If A is a skew-symmetric matrix which is also a square matrix then the determinant of A should satisfy the below condition.
We are given that Ais invertible and skew-symmetric. Consider 0 1 1 0. Show that B is not invertible.
Notice that any diagonal matrix is equal to its transpose and so such matrices are automatically symmetric. We want to prove the above theorem. Det A T det -A -1 n detA.
Then M-I is invertible iff A-frac1-cosasinaI is invertible. The determinant of skew symmetric matrix is non-negative. So M-I is definitely not invertible if ain S2kpi.
The determinant of a skew symmetric matrix of odd order is zero which means skew symmetric matrix of an odd number are singular. A matrix is called skew-symmetric if the transpose is equal to its negative. Thus A-1 is symmetric also.
If the matrix is invertible then the inverse matrix is a symmetric matrix. The inverse of a symmetric matrix happens to be the same as the inverse of any matrix. Endgroup amsmath Aug 31 19 at 1411.
The matrix inverse is equal to the inverse of a transpose matrix.

5 Write The Following Matrix A As The Sum Of A Chegg Com

Class 12th Maths Chapter 3 Matrices Part 1 All Basics Uses Of Matrix By Aman Youtube Class 12 Maths 12th Maths Teaching Mathematics

If A Is An Invertible Symmetric Matrix The A 1 Is A A Diagonal Matrix B Symmetric C S Youtube
Slide View 15 462 662 Fall 2020

A Matrix Is Skew Symmetric Of A T A Prove That If Chegg Com

The Inverse Of An Invertible Symmetric Matrix Is A Symmetric Matrix Youtube
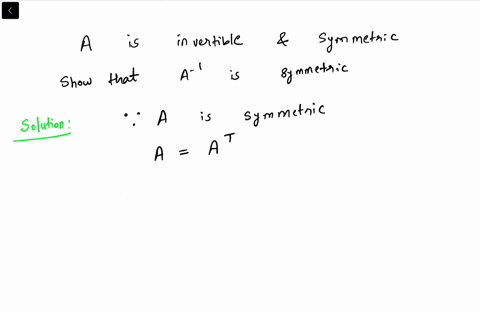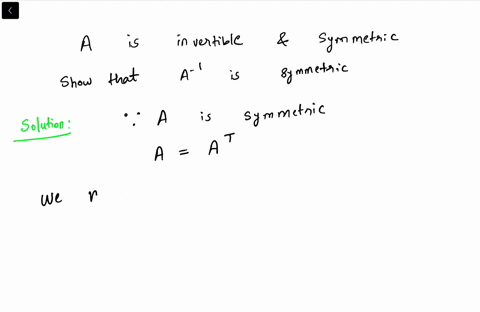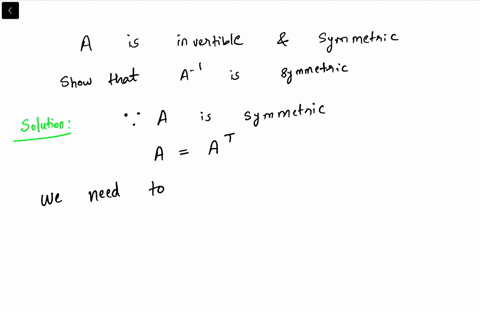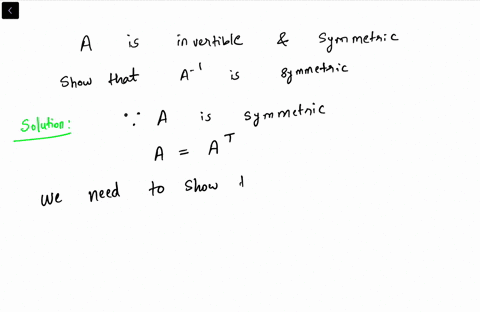
Solved Use Properties Of The Inverse To Prove The

For Any N X N Matrices A And B Prove That A Aa Is Chegg Com

Class 12th Maths Chapter 3 Matrices Exercise 3 2 Questions 18 To 22 Solutions By Aman Class 12 Maths Teaching Mathematics This Or That Questions

Skew Symmetric Matrix Don T Memorise Youtube

Answered Mam Is Similar To A If And Only If M Bartleby

The Determinant Of A Skew Symmetric Matrix Is Zero Problems In Mathematics
Https Lcvmwww Epfl Ch Teaching Modelling Dna Index Php Dir Exercises File Corr02 Pdf
Solved 4 4 3 17 Let A Be A Skew Symmetric Matrix That Chegg Com

Class 12th Mathematics Chap 3 Matrices Part 9 Transpose Symmetric And Skew Symmetric Matrix Youtube Mathematics Class Matrices Class 12

Q13 Suppose A And B Are Skew Symmetric Matrices At Chegg Com

Solved A Every 3 X 3 Skew Symmetric Matrix Is Not Inver Chegg Com
Q4 7 Points Part A 3 Points For What Value S Chegg Com

The Determinant Of A Skew Symmetric Matrix Is Zero Problems In Mathematics

