Kernel Of Matrix Multiplication
- Inside clBlas - clBlas on AMD. Vectors can be added together or multiplied by a real number For vw 2V a 2R.

The Fourier Transform Can Be Computed As A Matrix Multiplication Physics And Mathematics Cool Math Tricks Math Tricks
The kernel of the matrix U U U at the end of the elimination process which is in reduced row echelon form is computed by writing the pivot variables x 1 x 2 x_1x_2 x 1 x 2 in this case in terms of the free non-pivot variables x 3 x_3 x 3 in this case.

Kernel of matrix multiplication. Here is the transpose kernel which we used. To extend this into a full matrix-vector multiplication the OpenCL runtime maps the kernel over the rows of the. Are special kinds of sets whose elements are called vectors.
Matrix multiplication Matrix inverse Kernel and image Radboud University Nijmegen From last time Vector spaces VW. 631 Mul Mul takes as input. The complete source-code is available at GitHub.
AbstractSparse-sparse matrix multiplication SpGEMM is a computation kernel widely used in numerous application domains such as data analytics graph processing and scientific comput-ing. Mul a host function serving as a wrapper to Muld. D_Pxy 𝝨 d_Mxkd_Nky for k012width.
You compute a multiplication of this sparse matrix with a vector and convert the resulting vector which will have a size n-m12 1 into a n-m1 square matrix. I am pretty sure this is hard to understand just from reading. In this work we propose MatRaptor a novel SpGEMM accelerator that is high performance and highly resource efficient.
Convolution is the process of adding each element of the image to its local neighbors weighted by the kernel. 67 of people thought this content was helpful. 1 1 -4.
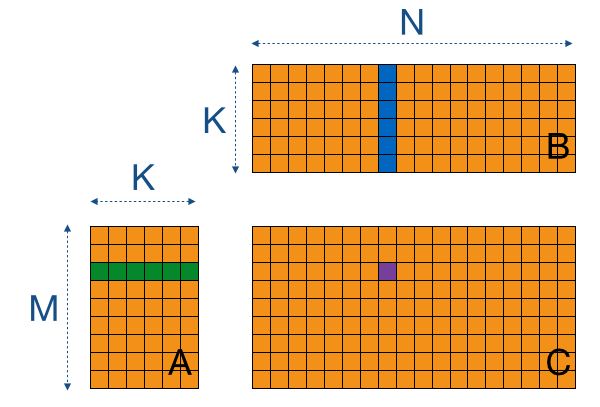
A jk M matrix multiplied by a kl N matrix results in a jl P matrix. Kernel A Free module of degree 3 and rank 1 over Integer Ring Echelon basis matrix. A B is the whole space.
The formula used to calculate elements of d_P is. Fortunately our kernel can be easily extended to a general matrix multiplication kernel. On the other hand there exist matrices A.
Which is equal to. Rn fa 1a n ja i 2Rg. Muld a kernel that executes the matrix multiplication on the device.
A and ker. Here is a constructed matrix with a vector. The idea is that this kernel is executed with one thread per element in the output matrix.
The kernel function matvec computes in each invocation the dot product of a single row of a matrix A and a vector x. Two pointers to host memory that point to the elements of A and B The height and width of A and the width of B. So here is an example for 22 kernel and 33 input.
Back to the top of the page. Well start with a very simple kernel for performing a matrix multiplication in CUDA. Creation of matrices and matrix multiplication is easy and natural.
V w 2V a v 2V The simplest examples are. A Matrix 1 2 3 3 2 1 1 1 1 sage. As such each thread ij iterates over the entire row i in matrix A and column j in matrix B.
For example there exist matrices A and B such that ker. In general we really cant tell anything about the nullspace of a sum of matrices just from knowing the matrices null spaces. The transpose kernel itself is actually quite trivial and is negligible in terms of computational cost compared to the main matrix-multiplication kernel.
- Introduction - Matrix-multiplication - Kernel 1 - Kernel 2 - Kernel 3 - Kernel 4 - Kernel 5 - Kernel 6 - Kernel 7 - Kernel 8 - Kernel 9 - Kernel 10 - Whats next. Const int ID0 get_group_id0TRANSPOSEX tx. This is related to a form of mathematical convolution.
B are both trivial but ker. A w -9 1 -2 sage. OpenCL SGEMM tuning for Kepler Note.
W A 0 0 0 sage. Currently our kernel can only handle square matrices. The matrix operation being performedconvolutionis not traditional matrix multiplication despite being similarly denoted by.
Matrix multiplication between a IxJ matrix d_M and JxK matrix d_N produces a matrix d_P with dimensions IxK. In general matrix multiplication is defined for rectangular matrices. The above condition is written in the kernel.
W vector 1 1 - 4 sage. It ensures that extra threads do not do any work. With the boundary condition checks the tile matrix multiplication kernel is just one more step away from being a general matrix multiplication kernel.
Opencl Matrix Multiplication Sgemm Tutorial

A Comprehensive Guide To Convolutional Neural Networks The Eli5 Way Deep Learning Data Science Learning Networking
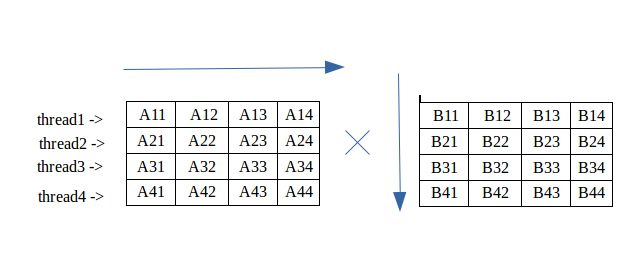
Multiplication Of Matrix Using Threads Geeksforgeeks
What Types Of Matrix Multiplication Are Used In Machine Learning When Are They Used Data Science Stack Exchange

Matrix Matrix Multiplication On The Gpu With Nvidia Cuda Matrix Multiplication Multiplication Matrix

Multiplication Kernel An Overview Sciencedirect Topics
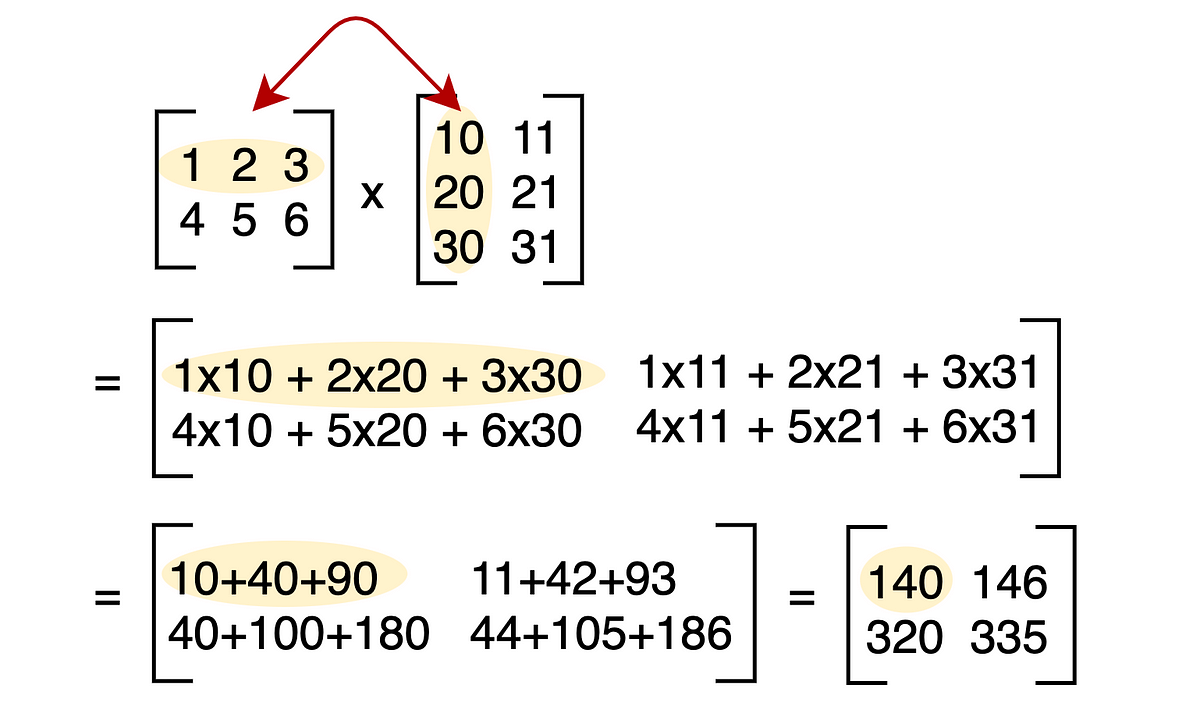
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

Blocked Matrix Multiplication Malith Jayaweera

A Sparse Matrix Multiplication Assembly Kernel The Compute Kernel Is Download Scientific Diagram

Matrix Multiplication 1 Cuda Matrix Multiplication Multiplication Matrix

Matrix Multiplication In C Applying Transformations To Images

Numpy Cheat Sheet Matrix Multiplication Math Operations Multiplying Matrices
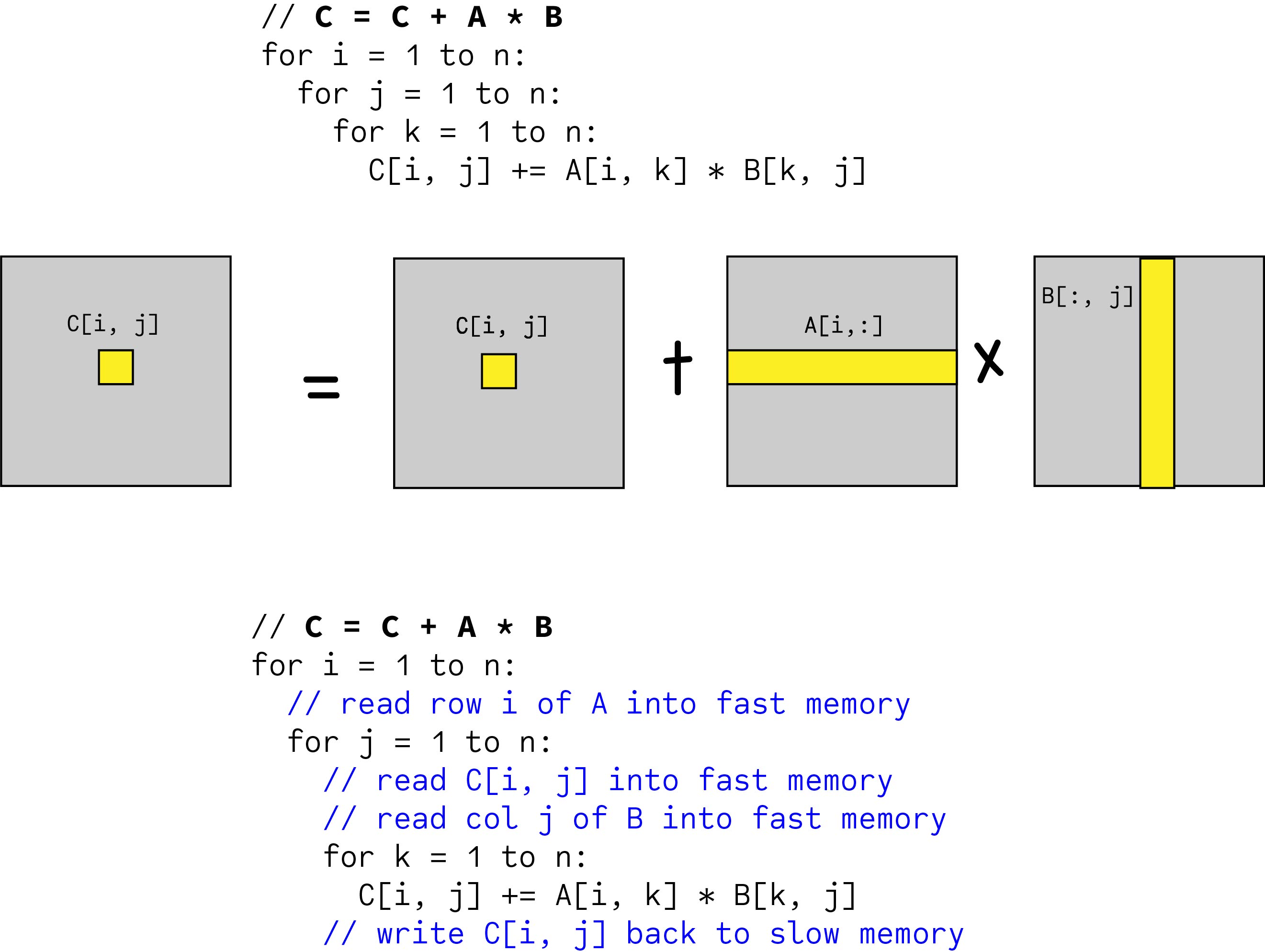
Blocked Matrix Multiplication Malith Jayaweera

Performing Convolution By Matrix Multiplication F Is Set To 3 In This Download Scientific Diagram

A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

2 D Convolution As A Matrix Matrix Multiplication Stack Overflow

Cannons Algorithm For Distributed Matrix Multiplication Matrix Multiplication Multiplication Algorithm

