Matrix Diagonalizable Condition

25 May, 2021

If an endomorphism is diagonalizable it is said to be diagonalizable by similarity. A matrix is diagonalizable by a unitary matrix if and only if it is a normal matrix.

Diagonalization On Linear Algebra

If A satisfies any polynomial p x without repeated roots ie.

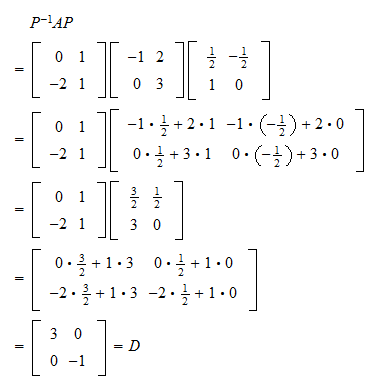
Matrix diagonalizable condition. The first condition is the case for almost all matrices. S 1 A S D then K A min G A S S 1 is called the spectral condition number of A. 608Diagonal matrices CAN have zeros along the main diagonal.

However thatAhasndistinct eigenvalues is a suﬃcient condition forAtobe diagonalizable. I kind of misspoke at 035. An n n matrix A is diagonalizable if it is similar to a diagonal matrix.

An -matrix is said to be diagonalizable if it can be written on the form where is a diagonal matrix with the eigenvalues of as its entries and is a nonsingular matrix consisting of the eigenvectors corresponding to the eigenvalues in. Gcd p x p x 1 then 3 holds so A is diagonalizable. By Proposition 232 matrix Ais diagonalizable if and only if there is a basis of R3 consisting of eigenvectors of A.

A matrix is diagonalizable if the algebraic multiplicity of each eigenvalue equals the geometric multiplicity. Sufficient Condition for Diagonalization If an nx n matrix A has n distinct eigenvalues then the. Condition number for matrix of eigenvectors of a diagonalizable matrix.

We define these terms state the relevant theo. Orthogonal matrix-real symmetric matrix- is Hermit matrix so diagonalizable. Find the eigenvalues of the matrix and determine whether there is a sufficient number to guarantee that the matrix is diagonalizable.

If is large checking for linear independence can be tedious. Nidentity matrixIis trivially diagonalizable for it is diagonal itself butit has a single eigenvalue the unit. A matrix or linear map is diagonalizable over the field F if and only if its minimalpolynomial is a product of distinct linear factors over F.

Corollary 169LetAbennIfAhasndistinct eigenvalues then it admitsnlinearly independent eigenvectors and thus it is diagonalizable. V V is diagonalizable if the sum of eigenspace dimensions is equal to dim V. We now know that an matrix is diagonalizable if and only if has linearly independent eigenvectors.

In particular the powers of a diagonalizable matrix can be easily computed once the matrices. Therefore the shear transformation is not diagonalizable. Hermit matrix-matrix which is equal to their conjugate transponse-is normal so diagonalizable.

Recall that the matrix may be diagonalizable even though it is not guaranteed to be diagonalizable by. A matrix is diagonal when all entries NOT on th. The matrix is diagonalizabel if and only if the sum of these dimensions is n.

Let A be a diagonalizable matrix ie A S D S 1. An n matrix is diagonalizable if the sum of the eigenspace dimensions is equal to n. That is if there exists an invertible n n matrix C and a diagonal matrix D such that A CDC 1.

Concerning the sentence There exists a matrix B and a diagonal matrix D such that. So lets nd the eigenvalues and eigenspaces for matrix A. A basis for cannot be constructed from the eigenvectors of the representing matrix.

A diagonalizable matrix is any square matrix or linear map where it is possible to sum the eigenspaces to create a corresponding diagonal matrix. Put in another way a matrix is diagonalizable if andonly if all of its elementary divisors are linear The following sufficient but not necessary condition is often useful. A linear map of T.

Otherwise compute the dimension of each eigenspace. For A being a diagonalizable matrix define G A S. D B 1 A B well.

There is a simple sufficient condition for diagonalizability. Matrix diagonalization is useful in many computations involving matrices because multiplying diagonal matrices is quite simple compared to multiplying arbitrary square matrices. Given two diagonalizable matrices they commute if and only if they can be diagonalized simultaneously that is if they share the same orthonormal basis of eigenvectors.

Skip to the 4 ways. For any matrix A condition number is defined as κ A A A 1. For example given any matrix A if you randomly perturb the entries then with probability 1 the resulting matrix has n distinct eigenvalues.

Normal matrices-those which commutate with its hermit matrix- are diagonalizable. If a n n matrix has n distinct eigenvalues then it is automatically diagonalizable.

Eigenvalues Eigenvectors 7 1 Eigenvalues Eigenvectors N N