Matrix Multiplication Complexity Is
However it is unknown what the underlying complexity actually is. Ae bg af bh ce dg and cf dh.

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
In this post we will be learning about different types of.

Matrix multiplication complexity is. The complete solution to axb. Ax b a11 a 21. 2 Calculate following values recursively.
So value of C11 consists of n multiplications and n-1 additions. For example if you multiply a matrix of n x k by k x m size youll get a new one of n x m dimension. As of December 2020 the matrix multiplication algorithm with best asymptotic complexity runs in On 23728596 time given by Josh Alman and Virginia Vassilevska Williams however this algorithm is a galactic algorithm because of the large constants and cannot be realized practically.
Using this library we can perform complex matrix operations like multiplication dot product multiplicative inverse etc. The naive algorithm has complexity Omjn for multiplying an m x j matrix by a j x n matrix or On3 for square n x n matrices. 1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram.
See the wikipedia article on matrix multiplication. People can look at algorithms and directly say what its time complexity is but I cant do that well. In other words no matter how we parenthesize the product the result will be the same.
The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. Bentuk matriks axb dan xab adalah salah satunya materi matriks yang terbilang mudah. Enter the 4 elements of first matrix.
The time complexity is ON 28074. Each cell has two operations which is multiplication and addition. 6 2 8 7 The first matrix is 5 6 1 7 The second matrix is 6 2 8 7 After multiplication 78 52 62 51 Complexity.
For example if we had four matrices A B C and D we would have. Here you can perform matrix multiplication with complex numbers online for free. Enjoy the videos and music you love upload original content and share it all with friends family and the world on YouTube.
In a single step. There are specifically adapted algorithms for say solving linear systems ax b for sparse matrices a such as the conjugate. Solvay Strassen algorithm achieves a complexity of On 2807 by reducing the number of multiplications required for each 2x2 sub-matrix from 8 to 7.
Matrix Multiplication in NumPy is a python library used for scientific computing. ABCD AB CD A BCD. The matrix multiplication complexity of text Mat_ ntimes ntimes n is the lowest computational complexity of evaluating the bilinear mapping text Mat_ ntimes ntimes n ie multiplying any two given ntimes n matrices in F ntimes n which is counted by the number of multiplications required to compute their matrix multiplication.
Their multiplication result is C. The best known algorithm has complexity approximately On23728639. Consider two n n matrices A and B.
Unless the matrix is huge these algorithms do not result in a vast difference in computation time. The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of On 23737. In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions.
There are d multiplications and d - 1 additions which equates to about 2d in. 5 6 1 7 Enter the 4 element of second matrix. Following is simple Divide and Conquer method to multiply two square matrices.
As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one. We have many options to multiply a chain of matrices because matrix multiplication is associative.

Systolic Arrays Algorithm For Matrix Multiplication Mathematics Stack Exchange

Matrix Chain Multiplication Dynamic Programming Youtube
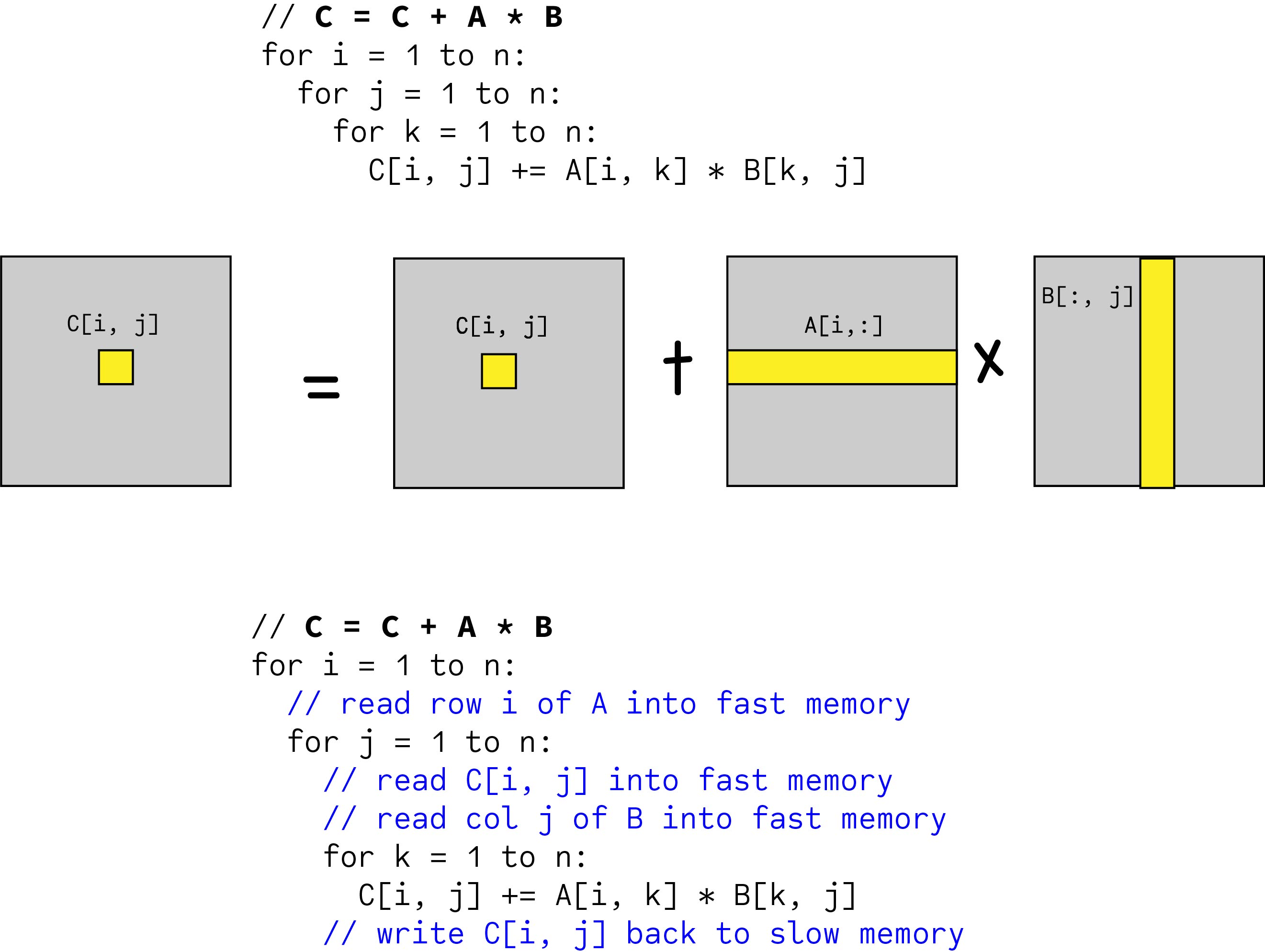
Blocked Matrix Multiplication Malith Jayaweera
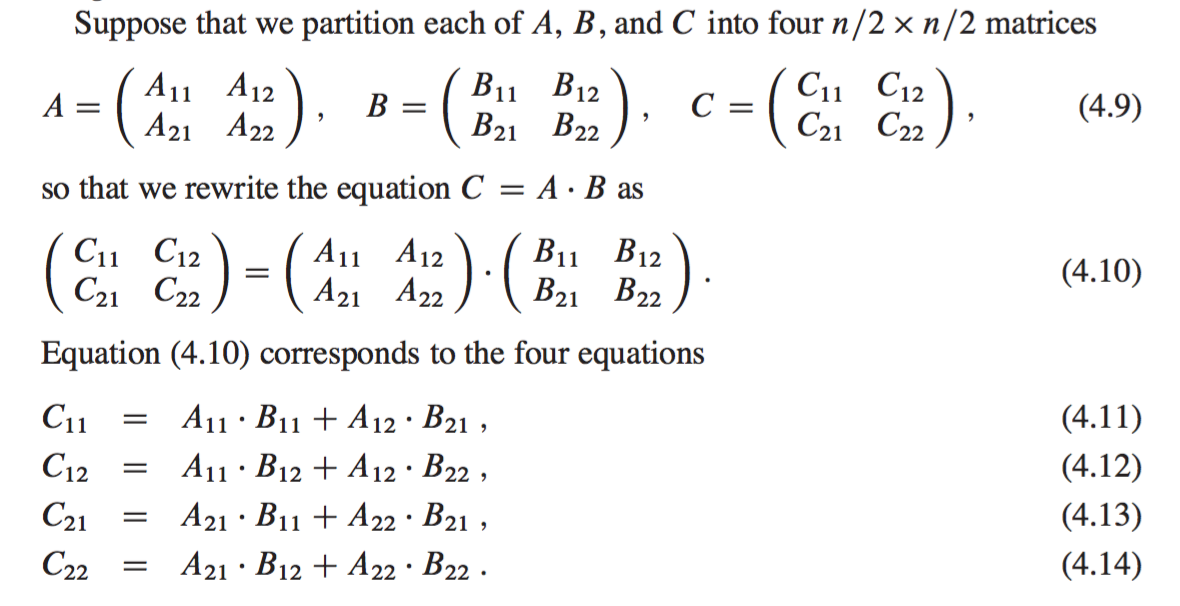
Matrix Multiplication Using The Divide And Conquer Paradigm
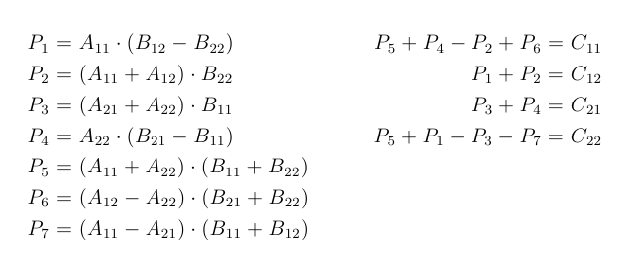
Strassen Matrix Multiplication C The Startup

Time Complexity Of Some Matrix Multiplication Mathematics Stack Exchange

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

2 9 Strassens Matrix Multiplication Youtube
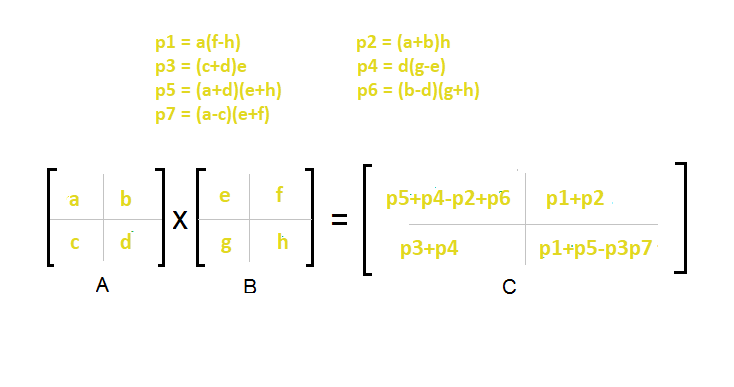
Strassen S Matrix Multiplication Algorithm

Matrix Multiplication Using The Divide And Conquer Paradigm
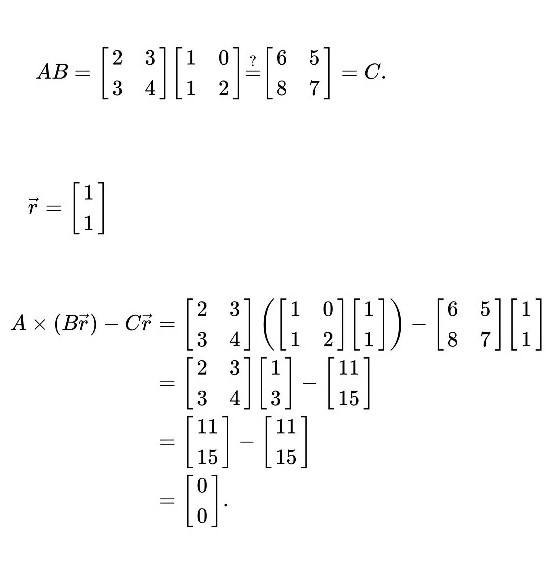
Freivalds Algorithm For Verifying Matrix Multiplication

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
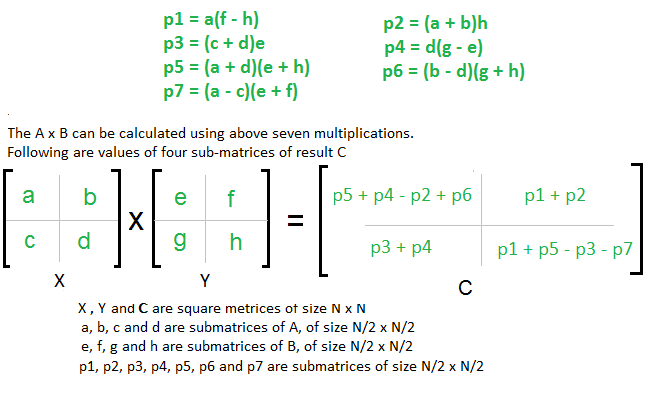
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange
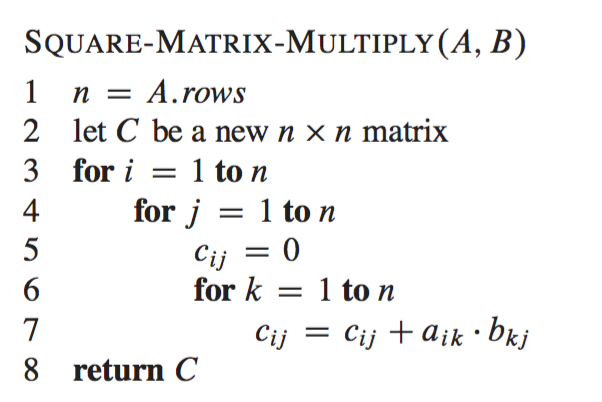
Matrix Multiplication Using The Divide And Conquer Paradigm

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm