Matrix Singular Value Rank
A full rank matrix will have a fairly small condition number. The matrix in a singularvalue decomposition ofAhas to be a 23 matrix so it must be 610 p0 0.

How To Calculate The Singular Values Of A Matrix Youtube
We call the associated estimator W.

Matrix singular value rank. Question 1 50 points. Adaptive shrinkage of singular values 4 is de ned for a positive threshold and encompasses soft thresholding 4 for 1 and hard thresholding 2 when 1. EFG BCD 7 7 where7 is the largest singular value and 7 is the smallest singular value If the matrix is rank deficient.
If the matrix is full rank. 4 3 1 1 2 125 0 8 6 8 6 5 2 1 0 0 6 8. In fact we can compute that the eigenvalues are 1 3602p 90 pand3p 0.
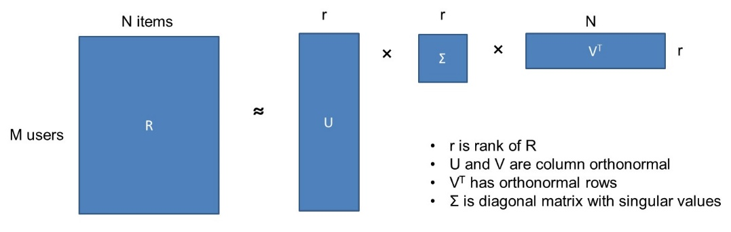
Now the rank one decomposition of A is and the rank one decomposition of B is. A singular value decomposition SVD of a matrix is a factorization where and are orthogonal where and. The rank of a matrix cannot exceed the number of its rows or columns.
As we will see in Chapters 7 15 and 23 finding the rank of an arbitrary matrix is somewhat complex and relies on the computation of what are termed its singular values. Diagonalization of a matrix Ais of the form A VDV where the columns of V are eigenvectors of Aand form an orthonormal. 101 Eigenvalue and Singular Value Decompositions An eigenvalue and eigenvector of a square matrix A are a scalar λ and a nonzero vector x so that Ax λx.
The maximum number of its linearly independent columns or rows of a matrix is called the rank of a matrix. The singular values of a singular matrix will contain one or more zeros. Adding a column z to a matrix A R m n m n will cause the min singular value σ m i n to decrease or stay the same ie σ m i n A z σ m i n A.
But the value 001 is so small that A is nearly a rank two matrix. A singular value and pair of singular vectors of a square or rectangular matrix A are a nonnegative scalar σ and two nonzero vectors u. EF.
The other must equal the trace so σ 1 2 125. The condition number of a matrix is the ratio of its largest and smallest singular values. For any m n matrix rank A nullity A n.
However the Euclidean projection onto Ck can be computed efficiently using. Numerical results based on simulation. Up to 10 cash back In this paper we propose an iterative singular value p-shrinkage thresholding algorithm for solving low rank matrix recovery problem and also give its two accelerated versions using randomized singular value decomposition.
After finding unit vectors perpendicular to u1 and v1 basis vectors for the left nullspace and nullspace respectively we see that the SVD of A is. S svd A returns the singular values of matrix A in descending order. U A V Σ.
If a row of zeros occurs the rank of the matrix is less than n and it is singular. RARMP The hardness of the above problem mainly comes from the non-convexity of the set of low-rank matrices Ck. The singular value decomposition SVD of a matrix is similar to the diagonalization of a normal matrix.
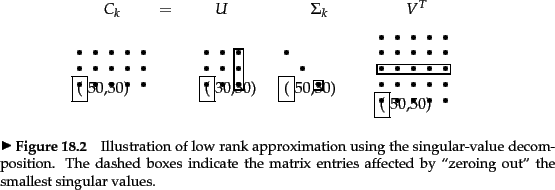
So you see that if A has a small singular value then you can get a lower rank matrix B close to A by setting the small singular value to zero. Note that as a byproduct the rank of the matrix is also estimated as R P. Advanced Math questions and answers.
The SVD reveals a great deal about a matrix. Matrices that are close to singular will contain singular values very close to zero. We know that at least one of the eigenvalues is 0 because this matrix canhave rank at most 2.
The singular value decomposition theorem shows that every matrix is diagonal provided one uses the proper bases for the domain and range spaces. Thus the singular values ofAare1360 610290 310 and3 0. Singular value decomposition SVD of a full row rank matrix Consider the matrix A.
MinXNP i1 U i i max 1 i0 V0 9 the adaptive trace norm estimator ATN with 0 and 1. We can diagonalize A A by UAV Σ. If we consider a square matrix the columns rows are linearly independent only if the matrix is nonsingular.
In fact the matrix B was created by setting that last singular value to zero. The convergence result of the proposed singular value p-shrinkage thresholding algorithm is proved. Because this is a rank 1 matrix one eigenvalue must be 0.
Diagonalization of a matrix decomposes the matrix into factors using the eigenvalues and eigenvectors. 21 Singular Value Decomposition SVP Consider the following more robust formulation of ARMP RARMP min X ψX 1 2 AXb2 2 st XCk X.

Finding Lu Decomposition Algebra Math Math Equations

Singular Value Decomposition In Recommender Systems Dataminingapps

How To Calculate The Singular Values Of A Matrix Youtube
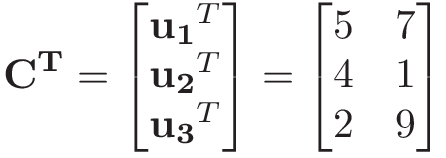
Understanding Singular Value Decomposition And Its Application In Data Science By Reza Bagheri Towards Data Science
009 The Singular Value Decomposition Svd Illustrated In Python Master Data Science

Homogeneous Equation Algebra Equation Math

Understanding Entanglement With Svd

Singular Value Decomposition Svd Matrix Approximation Youtube

If A Matrix Has Singular Square Submatrix Then No Lu Decomposition Algebra Math Column

Intro To Eigen Values Intro Algebra Math
009 The Singular Value Decomposition Svd Illustrated In Python Master Data Science

How To Calculate The Singular Values Of A Matrix Youtube
Singular Value Decomposition In Recommender Systems Dataminingapps

Term Document Matrices And Singular Value Decompositions
Lecture 49 Svd Gives The Best Low Rank Approximation Advanced Stanford Youtube
009 The Singular Value Decomposition Svd Illustrated In Python Master Data Science