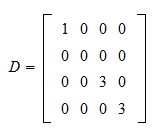Multiply Diagonal Matrix
Multiplying only diagonal elements of a matrix. Both approaches are naturally much faster than calculating product and then taking the diagonal.

1 7 Diagonal Triangular And Symmetric Matrices 1
For matrix multiplication the number of columns in the first matrix must be equal to the number of rows in the second matrix.

Multiply diagonal matrix. All you have to compute are the diagonal elements. If the condition is satisfied the total product is multiplied by the element that the traversal is on at that moment. Deducing a formula for multiplying a tri-diagonal symmetrical matrix with vectors.
Under Multiplication Diagonal Matrices are commutative i. PQ QP If P beginbmatrix 2 0 0 4 endbmatrix and Q beginbmatrix 4 0 0 3 endbmatrix P x Q beginbmatrix 80 0 0 0 0 120 endbmatrix beginbmatrix 8. A n n And a matrix A that is A with only the diagonal elements multiplied by values u 1 u 2 u n but the upper diagonal elements stay intact that is.
A 2 n. A nprandomrandom10001000 B nprandomrandom10001000 timeit npeinsumijji-i AB -- 207 ms 591 µs timeit sumAiBi for i in rangeAshape0 -- 168 ms 219 ms. To find the value of each of the diagonal.
I then discussed block diagonal matrices ie block matrices in which the off-diagonal submatrices are zero and in a multipart series of posts showed that we can uniquely and maximally partition any square matrix into block. Finally consider multiplying two diagonal matrices. A a 11 a 12.
Suppose that I gave a upper diagonal matrix A of the form. Create a matrix with the elements of v on the first super diagonal k1. When you specify a vector of length n as an input diag returns a square matrix of size nabs k.
The product of matrices A and B is denoted as AB. D d1e1 d2e2. Diagonal matrices as was explained earlier are square matrices.
In a previous post I discussed the general problem of multiplying block matrices ie matrices partitioned into multiple submatrices. Where dk a scalar is the kth diagonal entry of D and ek is a m x m matrix with all zeros except for a 1 in the kth position along the diagonal. That is matrices are multiplied row by column.
LetA aik be anmnmatrix and bkj be annpmatrix. Multiplication of diagonal matrices is commutative. This is more like a math-programming problem dealing with memory efficiency but I thought it would be nice to expose it here.
Within the inner loop of the traversal we apply the conditional statement to check whether the element belongs to the diagonal. Proposition Let be a matrix and a diagonal matrix. TheproductABisdefined to be thempmatrixC cij such thatcijPnaikbkj for.
Matrix multiplication The product of matrices AandBis defined if thenumber of columns inAmatches the number ofrows inB. In mathematics particularly in linear algebra matrix multiplication is a binary operation that produces a matrix from two matrices. The product AB is defined to be the mp matrix C cij such that cij Pn k1 aikbkj for all indices ij.
A 1 n 0 u 2 a 22. By a diagonal matrix A. A d 1 s 1 s 1 d 2 s 2 s 2 s n 1 s n 1 d n.
The successive rows of the original matrix are simply multiplied by successive diagonal elements of the diagonal matrix. Then the product is a matrix whose -th row is equal to the -th row of multiplied by for every. U n a n n.
In this case all the off diagonal elements are assigned zero. Let A aik be an mn matrix and B bkj be an np matrix. The resulting matrix known as the matrix product has the number of rows of the first and the number of columns of the second matrix.
Multiplying two or more diagonal matrices produces a diagonal matrix. A 2 n. A 1 n 0 a 22.
What is the effect of post-multiplying a matrix by a diagonal matrix A. Let A R n n be a tri-diagonal symmetrical matrix like so. Here we traverse the matrix twice once for each diagonal.
Multiplication by a diagonal matrix Two useful results about products involving diagonal matrices are reported below. A u 1 a 11 a 12. If A and B are diagonal then C AB BA.
The result is a 6-by-6 matrix. Matrix multiplication The product of matrices A and B is defined if the number of columns in A matches the number of rows in B. You can express D as a sum of elementary basis functions.
D1 diag v1 D1 66 0 2 0 0 0 0 0 0 1 0 0 0 0 0 0 -1 0 0 0 0 0 0 -2 0 0 0 0 0 0 -5 0 0 0 0 0 0. The effect is that of multiplying the i-th row of matrix A by the factor k i ie.

Product Of Two Diagonal Matrices Is Diagonal Youtube
Introduction To Diagonal And Symmetric Matrices Unit And Orthogonal Vectors Using Python Numpy Examples And Drawings

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download
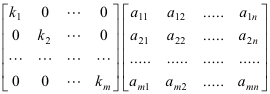
Effect Of Multiplying A Matrix By A Diagonal Matrix

Diagonal Matrix Definition Examples And Its Properties

Matrices Matrices A Matrix Is A Rectangular Array
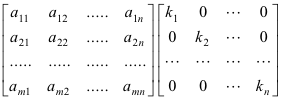
Effect Of Multiplying A Matrix By A Diagonal Matrix
Is A Diagonal Matrix With All Diagonal Entries As 1 An Identity Matrix Quora
Is A Diagonal Matrix With All Diagonal Entries As 1 An Identity Matrix Quora
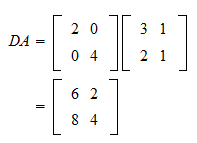
Multiplication By A Diagonal Matrix

Basis For The Definition Of A Diagonal Matrix Mathematics Stack Exchange

1 7 Diagonal Triangular And Symmetric Matrices Ppt Download

7 1 Matrices Vectors Addition And Scalar Multiplication
Diagonal Matrices 17 6 Sideway Output To