Symmetric Matrix Diagonalisable
Assume A Q D QT with Q q 1. Show that A is an invertible matrix whose inverse is A-1 A.
Https Www Impan Pl Pmh Teach Algebra Additional Diagonal Pdf
85 Diagonalization of symmetric matrices Definition.
Symmetric matrix diagonalisable. A UDU 1 with Uorthogonal and Ddiagonal. There exists an orthogonal matrix P such that P1AP D where D is diagonal. More generally matrices are diagonalizable by unitary matrices if and only if they are normal.
Show that B is not invertible. A is diagonalizable because it is a symmetric matrix. If the matrix A is symmetric then its eigenvalues are all real TH 86 p.
By using this website you agree to our Cookie Policy. Then AQ Q D. -12 Points DETAILS LARLINALGSM 73016.
Diagonalization of Symmetric Matrices. A real symmetric matrix is diagonalizable. Ii Let B be a skew-symmetric n x n-matrix where n is odd.
To illustrate the theorem let us diagonalize the following matrix by an orthogonal matrix. The mathematical relation between a matrix and its diagonalized matrix is. Therefore the theorem is called theSpectral Theorem for real symmetric matrices.
Dierent eigenspaces are orthgonal to each otherIn fact a matrixAis orthogonally diagonalizable if andonly if it is symmetric. Two vectors u and v in Rn are orthogonal to each other if uv 0 or equivalently if uTv 0. I Let A be a diagonalizable n x n-matrix of eigenvalues - 1 and 1.
Also the set of eigenvectors of such matrices can always be chosen as orthonormal. Ie given a real symmetric matrixis diagonal for some orthogonal matrix. A matrix is diagonalizable iff it is similar to a diagonal matrix.
A is a symmetric matrix if AT A Definition. Equivalently the matrix is equal to its transpose A A T. 366 A is orthogonally diagonalizable ie.
This is sometimes written as u v. A is diagonalizable because it is an anti-diagonal matrix. A matrix P is said to be orthogonal if its columns are mutually orthogonal.
The set of eigenvalues of a matrix is sometimescalled the spectrum of the matrix and orthogonal diagonalization of a matrix E factors Ein away that displays all the eigenvalues and their multiplicities. Show that n is even. The dimension of theeigenspace is the multiplicityofas a root of detAI.
Free Matrix Diagonalization calculator - diagonalize matrices step-by-step This website uses cookies to ensure you get the best experience. A square matrix A a i j is a symmetric matrix if its entries opposite the main diagonal are the same that is if a i j a j i for all i and j. Symmetric and hermitian matrices which arise in many applications enjoy the property of always being diagonalizable.
Enter your answers as a comma-separated list. A diagonalizable matrix is a square matrix that can be transformed into a diagonal matrix that is a matrix filled with zeros except for the main diagonal. The zero matrix 0 has that property so it is a symmetric matrix.
Let A be a square matrix of size n. 369 EXAMPLE 1 Orthogonally diagonalize A 12 21. Here is a shortcut to nd the eigenvalues.
Q n orthogonal and D diagd 1. A real matrix Ais symmetric if and only if Acan be diagonalized by an orthogonal matrix ie. Of course symmetric matrices are much more special than just being normal and indeed the argument above does not prove the stronger result that symmetric matrices are orthogonaly diagonalizable.
A matrix P is said to be orthonormal if. A matrix A 2Rn is symmetric if and only if there exists a diagonal matrix D 2Rn and an orthogonal matrix Q so that A Q D QT Q 0 B B B 1 C C C A QT. Every symmetric matrix is orthogonally diagonalizable.
The namethe spectral theoremis inspired by anotherstory of the inter-relationship of math and physics The rst part is directly proved. The one that is useful here is. Q n diagd 1.
53 as we will see in our examples. Real symmetric matrices are diagonalizable by orthogonal matrices. In the case of the real symmetric matrix we see that.
Of course the result shows that every normal matrix is diagonalizable. A matrix A in MnR is called orthogonal if. D n d 1 q 1.
Q n q 1. A 2 4 1 1 1 1 1 1 1 1 1 3 5. Diagonalization of symmetric matrices Theorem.
Strangely enough the best way to prove this and I think Strangs proof is very good is to use complex matrices. 366 eigenvectors corresponding to distinct eigenvalues are orthogonal TH 87p. 22 Diagonalizability of symmetric matrices The main theorem of this section is that every real symmetric matrix is not only diagonalizable but orthogonally diagonalizable.
The diagonalization procedure is essentially the same as outlined in Sec. -2 5 Find the eigenvalues of the symmetric matrix. D n q n.
Iii Let C be an n x n-matrix such that C2 - In. We are now ready to prove our main theorem.
Http Accounts Smccd Edu Reuterdahlt Xtraparts Math 20270 Presentations 20spring 202017 Week 2016 Sections 20ppt 20and 20pdf Math 20270 207 1 Pdf

7 Symmetric Matrices And Quadratic Forms 7 1

Diagonalizable By An Orthogonal Matrix Implies A Symmetric Matrix Problems In Mathematics

Week 10 Symmetric Matrices And Orthogonal Diagonalization Youtube

3 A For An N X N Matrix A And A Natural Number K Chegg Com
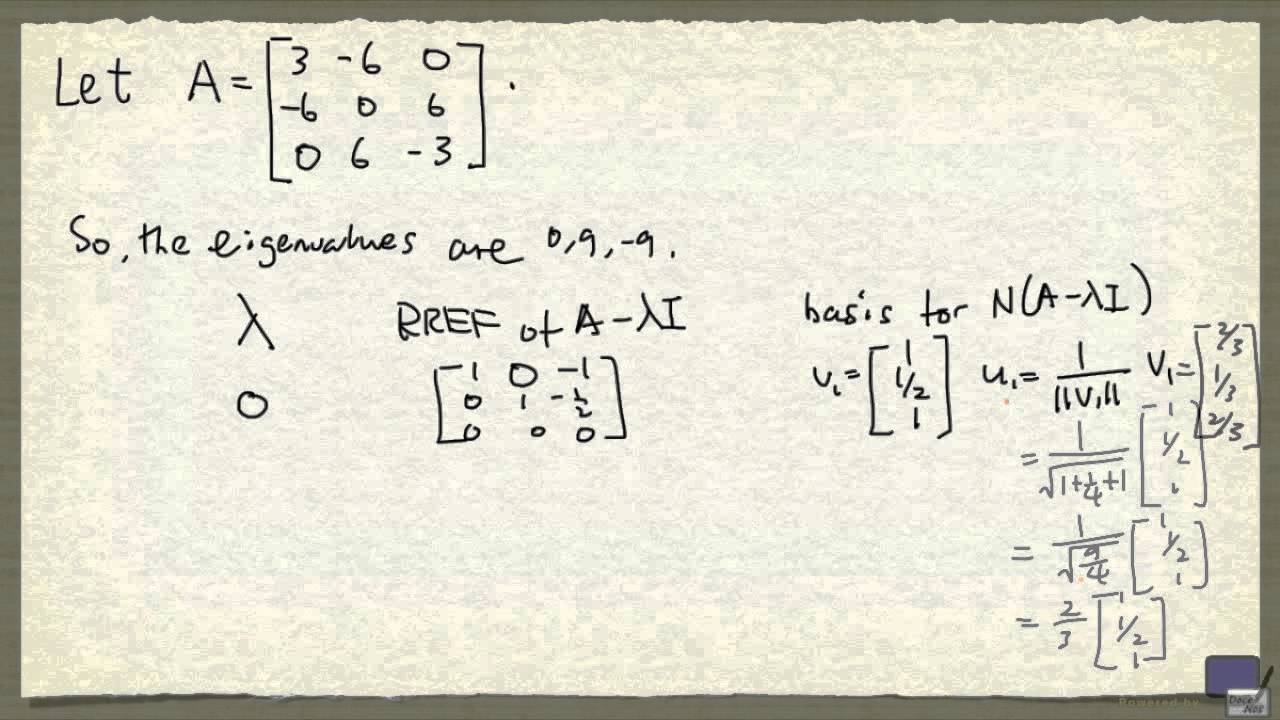
Week 10 Orthogonal Diagonalization Example Youtube

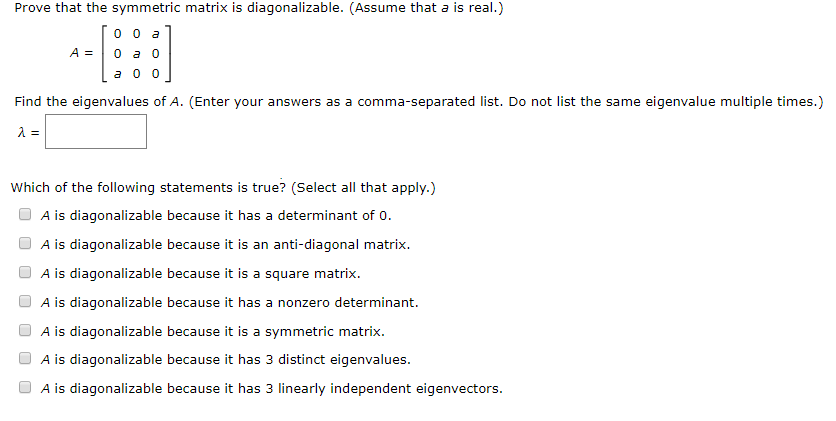
Prove That The Symmetric Matrix Is Diagonalizable Chegg Com

Diagonalization Of Symmetric Matrices Calcworkshop

Question About Diagonalizable Matrix Mathematics Stack Exchange
Chapter 10 3 Diagonalization Of Real Symmetric Matrices
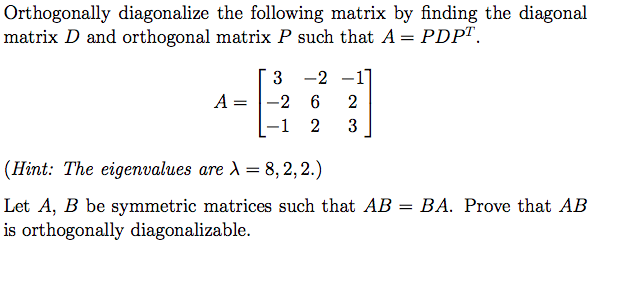
Orthogonally Diagonalize The Following Matrix By Chegg Com

Symmetric Matrices And Quadratic Forms Ppt Download

Linear Algebra Lecture 41 Diagonalization Of Symmetric Matrices Youtube

Proof For Why Symmetric Matrices Are Only Orthogonally Diagonalizable Mathematics Stack Exchange

Prove That The Symmetric Matrix Is Diagonalizable Chegg Com

Proof For Why Symmetric Matrices Are Only Orthogonally Diagonalizable Mathematics Stack Exchange

Linear Algebra Lecture 35 Diagonalizable Matrices Youtube

Showing A Matrix Is Not Diagonalizable Mathematics Stack Exchange
