Explain Parallel Matrix-vector Multiplication Algorithm With Example
Up to 10 cash back This way to compute graph algorithms is important for this work because. Int alg_matmul2Dint m int n int p float a float b float c int i j k.

Parallel Matrix Vector Multiplication Algorithm Download Scientific Diagram
Test performed in matrices with.
Explain parallel matrix-vector multiplication algorithm with example. Algorithm for Strassens matrix multiplication. Srandom time 0clock random. To capture interactions among tasks Node task Edgeundirecteddirected interaction or data exchange.
These algorithms are known to attain theoretical. K aij bikckj. Pragma omp parallel for.
Run sequential algorithm on a single processor core. A variant of Strassens sequential algorithm was developed by Coppersmith and Winograd they achieved a run time of On23753 The current best algorithm for matrix multiplication On2373 was developed by Stanfords own Virginia Williams5. I for j0.
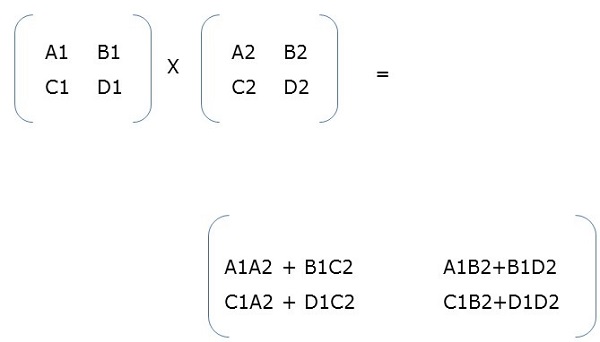
Matrix-Vector multiplication c0 a00 b0 a01 b1 a02 b2 a03 b3 a44 b4 c1 a10 b0 a11 b1 a12 b2 a13 b3 a14 b4 c2 a20 b0 a21 b1 a22 b2 a23 b3 a24 b4 c3 a30 b0 a31 b1 a32 b2 a33 b3 b34 b4 c4 a40 b0 a41 b1 a42 b2 a43 b3 a44 b4. Here we can see the code. For test the parallel algorithm were used the following number of cores.
3 matrixvector multiplication can be expressed with relational operators in a simple way. We primarily focus on Parallel Formulations Our goal today is to primarily discuss how to develop such parallel formulations. Allelization of matrix-vector operations and matrix-matrix multiplication as the driving examples.
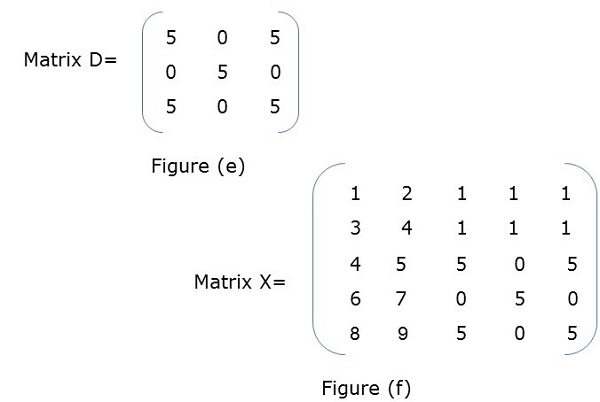
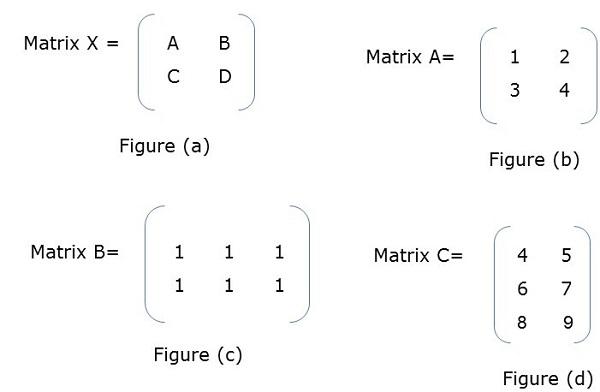
Matrix i malloc dimension sizeof TYPE. Partition b into four sub matrices b11 b12 b21 b22. GOOD NEWS FOR COMPUTER ENGINEERSINTRODUCING 5 MINUTES ENGINEERING SUBJECT -Theory Of Computation TOC Artificial Intelligen.
If this case the operation of inner multiplication of a row of the matrix A and the vector b can be chosen as the basic computational subtask. Algorithm Strassenn a b d begin If n threshold then compute C a b is a conventional matrix. Idea - Block Matrix Multiplication The idea behind Strassens algorithm is in the formulation.
12 Nov 2020 MapReduce is a technique in which a huge program is subdivided into small tasks and run parallelly to make computation faster save time and mostly used in distributed systems. Return 0. Parallel Algorithm May represent an entirely different algorithm than the one used serially.
The final step in the MapReduce algorithm is to produce the matrix A B. Broadcast and Reduction Algorithms. GOOD NEWS FOR COMPUTER ENGINEERSINTRODUCING 5-MINUTES ENGINEERING SUBJECT -Theory Of Computation TOC Artificial Intelligen.
From high school calculus. Matrix-vector multiplication 1063 It turns out that this algorithm uses only one parallel step more than the direct application of equation 1 starting from matrix P. The hypercube has 2d nodes and my_id is.
One can see that the overall number of steps to perform one iteration of Jacobi method is 2n 5 log n 1. Principles of Parallel Algorithm Design part 2 1. All of the algorithms described above are adaptations of the same algorithmic template.
Of course there will always be examples of parallel algorithms that were not derived from serial algorithms. 491625364964100 The results were obtained from the average over three tests of the algorithms. The reduce step in the MapReduce Algorithm for matrix multiplication.
Tasks generally share input output or intermediate data. This algorithm is used a lot so its a good idea to make it parallel. Matrix Multiplication With 1 MapReduce Step Last Updated.
1 provides a common framework for several graph problems. Else Partition a into four sub matrices a11 a12 a21 a22. 2 the challenges of parallel matrixvector multiplication are already known.
Recently research on parallel matrix-matrix multiplication algorithms have revisited so-called 3D algorithms which view processing nodes as a logical three-dimensional mesh. As the first example of parallel matrix computations let us consider the algorithm of matrix-vector multiplication which is based on rowwise block-striped matrix decomposition scheme. This extra step consists of the computation of the last component of xil.
A B C c ij k12n a ik c kj. Parallel p processors μ Amount of memory needed to store matrices Refs to remote memory Ω n3 pμ Irony Tiskin Toledo 04 If μ 3n2p one copy of A B C lower bound Ω n2 p words Achieved by Cannons algorithm 2D algorithm T P 2n 3p 4p α βn2p. We illustrate the algorithm for a hypercube but the algorithm as has been seen can be adapted to other architectures.
Originally there is only one copy of b tasks will have to communicate b.
Parallel Algorithm Matrix Multiplication Tutorialspoint
Parallel Algorithm Matrix Multiplication Tutorialspoint
C Dac Pune High Perf Comp Frontier Technologies Exploration Group And Cmsd University Of Hyderabad Technology Workshop Hypack October 15 18 2013
C Dac Pune High Perf Comp Frontier Technologies Exploration Group And Cmsd University Of Hyderabad Technology Workshop Hypack October 15 18 2013
Parallel Algorithm Matrix Multiplication Tutorialspoint

Parallel Matrix Vector Multiplication Algorithm Download Scientific Diagram
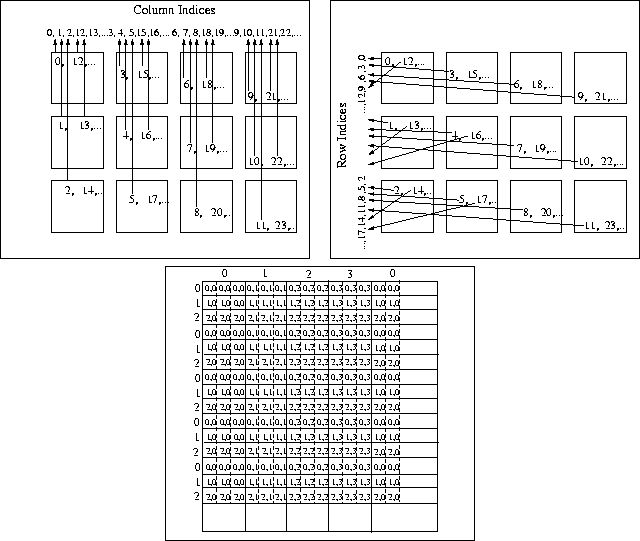
Analysis Of A Class Of Parallel Matrix Multiplication Algorithms
Mapreduce Algorithm For Matrix Multiplication
Section 8 1 Matrix Vector Multiplication

Parallel Matrix Multiplication C Parallel Processing By Roshan Alwis Tech Vision Medium

Sparse Matrix Vector Multiplication An Overview Sciencedirect Topics
Mapreduce Algorithm For Matrix Multiplication

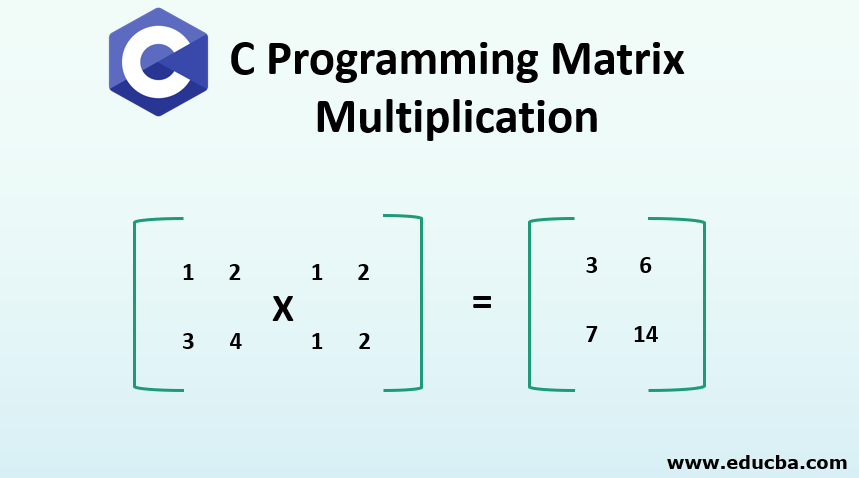
C Programming Matrix Multiplication C Program For Matrix Manipulation
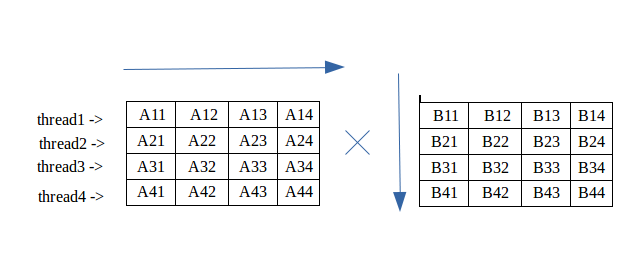
Multiplication Of Matrix Using Threads Geeksforgeeks
Parallel Matrix Multiplication C Parallel Processing By Roshan Alwis Tech Vision Medium

Matrix Matrix Multiplication Parallel Implementation Explained With Solved Example In Hindi Youtube

Actually Doing The Matrix Multiplication Intro To Parallel Programming Youtube

Parallel Matrix Vector Multiplication Algorithm Download Scientific Diagram
Mapreduce Algorithm For Matrix Multiplication