Matrix Chain Multiplication Questions Leetcode
Also Mii 0 as cost of multiplying a single matrix will be 0. Dp floatinf for i in rangelenarr for _ in rangelenarr taking care of diagonal with difference 0 for i in rangelendp.

Dp Problem Classifications Helpful Notes Leetcode Discuss
The minimum number of multiplications are obtained by putting parenthesis in following way ABCD -- 102030 103040 104030 Input.

Matrix chain multiplication questions leetcode. If you think of bursting a balloon as multiplying two adjacent matrices then this problem is exactly the classical DP problem Matrix-chain multiplication found in section 152 in the book Introduction to Algorithms 2nd edition. This article comprises of questions from Leetcode which can help you in your preparation for FAANG in just 30 days. Making A Large Island.
For i in 0. Given array nums 3158 Since bursting any baloon at any index say 1. We compute the optimal solution for the product of 2 matrices.
C 0ms Beats 100 both space and runtime Matrix chain multiplication dp. The number of operations are - 203010 402010 401030 26000. Let the input 4 matrices be A B C and D.
Ah I am stupid to have blocked the example with which I guided myself to code the matmul logicAnd the time complexity of my matmul method is just O no. N 4 arr 10 30 5 60 Output. The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7.
M ii 0 compute smallest matrix costs first for chains of length 2 to n. Therefore we can think of this problem as MAXIMIZING the operations in matrix chain multiplication. Example of Matrix Chain Multiplication.
If Mij represents the cost to multiply matrix ito matrix j then Mij Mik MK1j Pi-1 Pk Pj When calculating Mij. Let us proceed with working away from the diagonal. Mik and Mk1j should be already available this is called bottom-up filling of a matrix.
Let cost optmik. Find the best order for matrix chain multiplication. J i l-1 j is the endpoint of the chain.
Say the matrices are named as A B C D. Let j i lg optmij Naturalhigh for k in i. Let n optdimshigh optm newSeqWithn newSeqNaturaln opts newSeqWithn newSeqNaturaln for lg in 1.
Actually this problem looks quite troublesome at first after we dive in we will find out that this problem is actually a deformed version of Matrix Chain MultiplicationFor example. Assume that multiplying a matrix G 1 of dimension pq with another matrix G 2 of dimension qr requires pqr scalar multiplications. List int - int.
Out of all possible combinations the most efficient way is A BCD. Feel free to comment incase i missed any important question. Computing the product of n matrices G 1 G 2 G 3.
We know M i i 0 for all i. N len p -1. M 0 for x in xrange 0 n for y in xrange 0 n s 0 for x in xrange 0 n for y in xrange 0 n for i in xrange 0 n.
I collected these questions from bunch of resources online striver and are based on past interviews. Introduction Summary Validate Binary Search Tree Isomorphic Strings Read N Characters Given Read4 II - Call multiple times Read N Characters Given Read4 Number of Islands II. January 11 2017 342 AM.
Insert Delete GetRandom O 1 - Duplicates allowed. If you think of bursting a balloon as multiplying two adjacent matrices then this problem is exactly the classical DP problem Matrix-chain multiplication found in section 152 in the book Introduction to Algorithms 2nd edition. G n can be done by parenthesizing in different ways.
We need to compute M ij 0 i j 5. Dp i i0 taking care of diagonal with difference 1 for i in range0 lendp-1. We are given the sequence 4 10 3 12 20 and 7.
For l in xrange 2 n 1. Expand nums array by adding 1 at begining and end as bursting first and last baloon is similar to multiplication 1Xcurrent valueXnext value or prev valueXcurrent valueX1. For i in xrange 0 n-l 1.
Count of Smaller Numbers After Self. For example given 358 and bursting 5 the number of coins you get is the number of scalar multiplications you need to do to multiply two. P 10 20 30 Output.
6000 There are only two matrices of dimensions 10x20 and 20x30. Set Intersection Size At Least Two. 3X1X5 is similar to matrix multiplication 3X1 and 1X5.
For example in the matrix multiplication. The matrices have dimensions 1030 305 560. For example given 358 and bursting 5 the number of coins you get is the number of scalar multiplications you need to do to multiply two matrices A35 and B.
Define G i G i1 as an explicitly computed pair for a given paranthesization if they are directly multiplied.

Dynamic Programming Detailed Matrix Multiplication Case Java Code Implementation Programmer Sought

Massive Algorithms Matrix Chain Multiplication
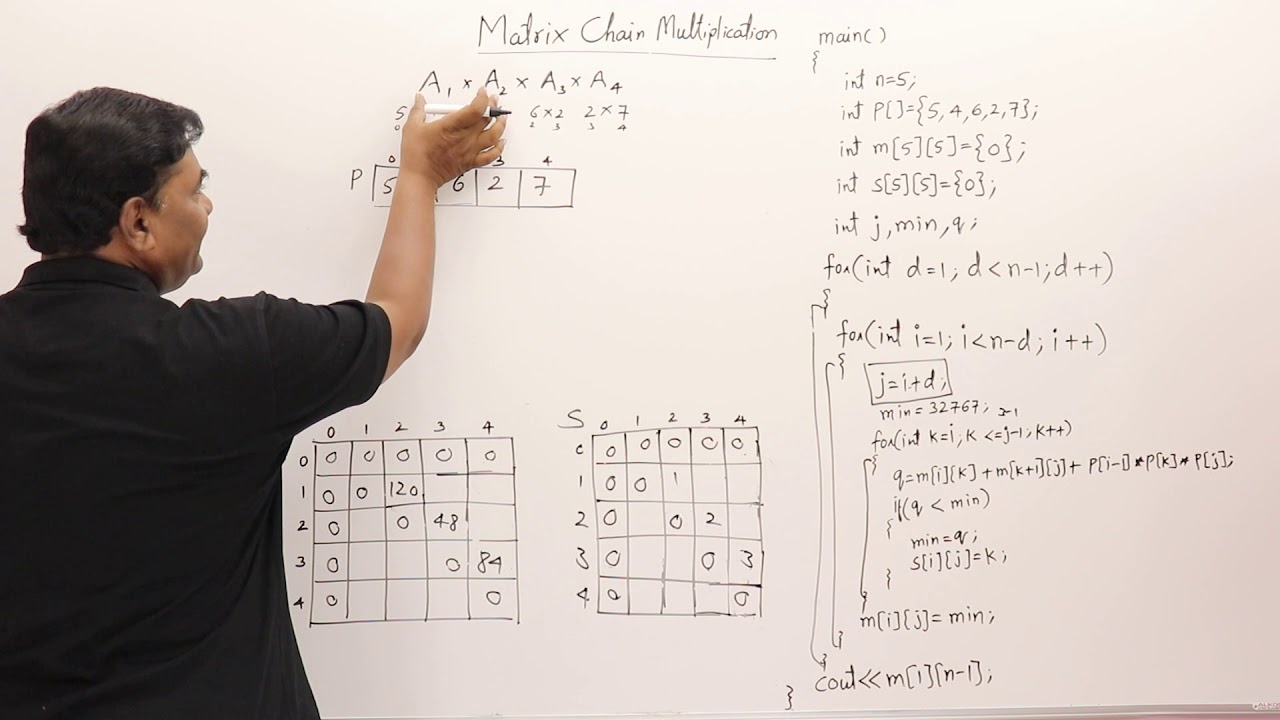
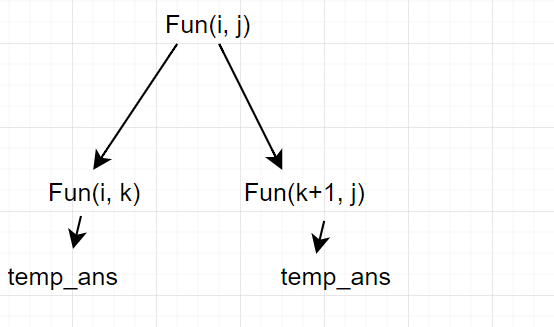
Dp Matrix Chain Multiplication With Comments And Reference Leetcode Discuss
Matrix Chain Multiplication Problem With Template And Code Explanation By Sirmihirmsd The Startup Medium

Massive Algorithms Matrix Chain Multiplication

Dynamic Programming 1 Matrix Chain Multiplication Programmer Sought

Leetcode Matrix Chain Multiplication Archives Algorithms And Me

Massive Algorithms Matrix Chain Multiplication
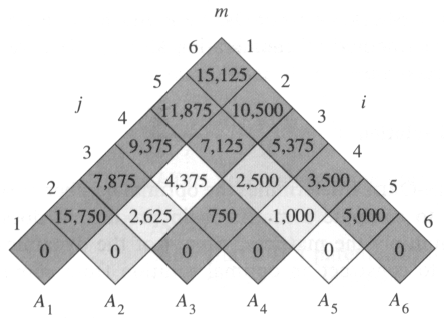
How To Solve Matrix Chain Multiplication Using Dynamic Programming Algorithms Blockchain And Cloud
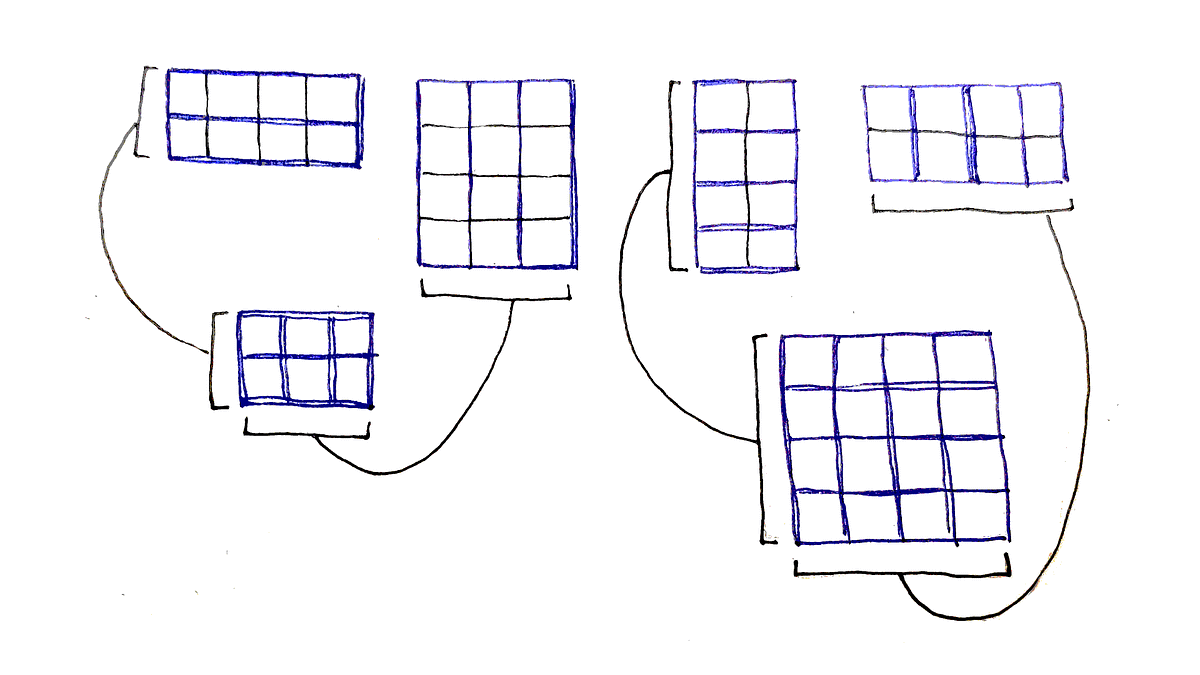
Matrix Chain Multiplication Problem With Template And Code Explanation By Sirmihirmsd The Startup Medium
Dynamic Programming Detailed Matrix Multiplication Case Java Code Implementation Programmer Sought

Leetcode Matrix Chain Multiplication Archives Algorithms And Me

Matrix Chain Multiplication Dynamic Programming Youtube
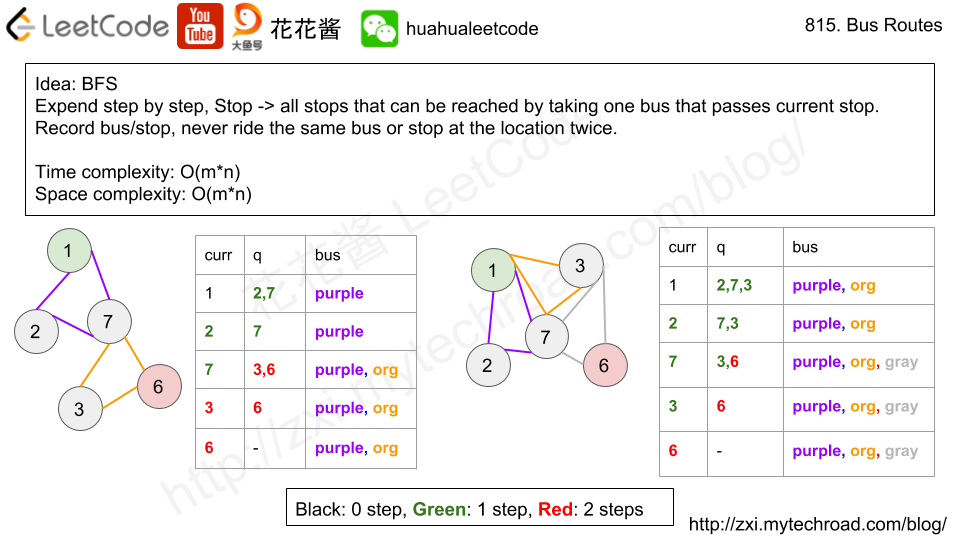
Massive Algorithms Leetcode 815 Bus Routes

Matrix Chain Multiplication Using Recursion Mcm Youtube

Massive Algorithms Matrix Chain Multiplication

Matrix Chain Multiplication Problem With Template And Code Explanation By Sirmihirmsd The Startup Medium

Leetcode Matrix Chain Multiplication Archives Algorithms And Me

Matrix Chain Multiplication Dynamic Programming Design Algorithms Lec 43 Bhanu Priya Youtube
