Properties Of Skew Symmetric Matrix Pdf

The diagonal of skew symmetric matrix consists of zero elements and therefore the sum of elements in the main diagonals is equal to zero. Thus ER 1 and ER 1 are the subspaces of Cnn consisting respectively of R-symmetric and R-skew symmetric vectors.

Pdf Computing Exponentials Of Skew Symmetric Matrices And Logarithms Of Orthogonal Matrices

A square matrix A is symmetric if ATA or A_ijA_ji.

Properties of skew symmetric matrix pdf. The eigen values of a skew Hermitian matrix are all purely imaginary or zero. X ij -x ji for all values of i and j. Themappingu u isbyinspectionlinearandinvertible.

Throughout the paper we write MT for the transpose of a matrix M and u for the conjugate transpose of a complex vector u. All main diagonal entries of a skew-symmetric matrix. In this section we provide bounds for the eigenvalues of the preconditioned matrix.

Let Abe a real symmetric matrix of size d dand let Idenote the d didentity matrix. The right conditions is BA-AB anticommute ABTBTA BA. We say that A Cmn is RS-symmetric RS-skew.

If λ is an eigenvalue of B Cnn let EB λ denote the λ-eigenspace of B. Thus skew Hermitian matrices satisfy kH -k just as skew symmetric matrices satisfy kT - k Where H denotes the conjugate transpose of a matrix. 26 2005 748757 Abstract.

Or Take a Test. The matrix U is called an orthogonal matrix if UTU I. The main diagonal of any skew-symmetricmatrix is zero sinceaiiaiiAny square matrix can be decomposed into a sum of a symmetric matrix and askew-symmetric matrix.

Scalar product of skew-symmetric matrix is also a skew-symmetric matrix. Q T -Q. Equal to its negative.

Also A0A 0 means that matrix A is symmetric positive definite respectively semidefinite. Skew symmetric matrix is a square matrix Q x ij in which i j th element is negative of the j i th element ie. U v 2 4 u 2v 3 u 3v 2 u 3v 1 u 1v 3 u 1v 2 u 2v 1 3 5 1 Fromtheequalityaboveonecanseethatthefollowingskewsymmetricmatrix u 2 4 0 u 3 u 2 u 3 0 u 1 u 2 u 1 0 3 5 2 satisfiesu v u v.

AB is symmetric in fact. When a matrix is in reduced row echelon form it is possible to tell how may solutions there are to the system of equations. Every real n -by- n matrix B is skew symmetric if and only if Dot B.

CHARACTERIZATION AND PROPERTIES OF RS-SYMMETRIC RS-SKEW SYMMETRIC AND RS-CONJUGATE MATRICES WILLIAM F. If Ais a square matrixB AAT2is symmetricC is skew-symmetric andABAAT2. Use up and down arrows to select.

De nition 1 Let U be a d dmatrix. X y Dot x B. A is skew-symmetric if AT-A or A_ij- A_ji.

AT1 AT0 0 1 b All the skew-Hermitian solutions of 31 are real skew-symmetric if and only if B0 B1 A0 r B1 B0 A1 4r A 2n AT1 AT0 0 or equivalently. Properties of Skew Symmetric Matrix. Now you can write x A x in a different way - it is just notation but I believe that it helps in this case -.

A matrix is skew-symmetric if and only if it is the opposite of its transpose. In other words a square matrix Q which is equal to negative of its transpose is known as skew-symmetric matrix ie. A matrix is symmetric if and only if it is equal to its transpose.

A a b a A b where a and b are vectors A is a matrix and by the dot I mean the inner product defined by a b a i b i. TRENCH SIAM J. 1 Properties of skew symmetric matrices 1.

The skew-symmetric property The matrix M q2Cqq is skew-symmetric. The possibilities are 1 no solutions - the last element in a row is non-zero and the. AB skew-symmetric ABTBTAT -B-ABA AB iff A and B commute.

Try to use the property through which the transpose matrix is defined ie. Borhaug 2008 this is. This implies that UUT I by uniqueness of inverses.

Thus if the Euler angles are used to represent the attitude of the vehicle as in Fossen 2002. We will say that a vector z Cn is R-symmetric R-skew symmetric if Rz z Rz z. When we add two skew-symmetric matrices then the resultant matrix is also skew-symmetric.

For every square matrix A the matrix A - Transpose A is skew symmetric. MatrixForm B A - Transpose A 0 4 3 0 4 0 2 1 3 2 0 5 0 1 5 0 1 B Transpose B True. Let R C m and S C n be nontrivial involutions.

PROPERTIES Their properties follow immediately from their close link to Hermitian Matrices. All entries above the main diagonal of a symmetric matrix are reflected into equal entries below the diagonal. Property 1 is true only when there are no singularities present in the formulation.

Perhaps the most important and useful property of symmetric matrices is that their eigenvalues behave very nicely. 0 suggestions are available. Ie R R1 6 Im and S S1 6 In.

Class 12 Symmetric And Skew Symmetric Matrices Youtube

Gate Ese Real Matrices Symmetric Skew Symmetric Orthogonal Matrices Offered By Unacademy

Https Lcvmwww Epfl Ch Teaching Modelling Dna Index Php Dir Exercises File Corr02 Pdf

Pdf A Note On The Stable Decomposition Of Skew Symmetric Matrices

Cbse Class 12 Symmetric And Skew Symmetric Matrices Elementary Operations And Invertible Matrices Offered By Unacademy

Skew Symmetric Matrix An Overview Sciencedirect Topics

Pin On Top Trending

Gate Ese Square Matrix As A Sum Of Symmetric And Skew Symmetric Matrix Offered By Unacademy

Symmetric And Skew Symmetric Matrix Theorems Videos And Examples

Pin On Mathematics

Mathematics Symmetric Skew Symmetric And Orthogonal Matrix Youtube

Pdf Symmetric And Skew Symmetric Block Kronecker Linearizations

Eigenvalues Of Real Skew Symmetric Matrix Are Zero Or Purely Imaginary And The Rank Is Even Problems In Mathematics

Hermitian And Skew Hermitian Matrix Youtube

Iit Jee Symmetric And Skew Symmetric Matrix Theorem In Hindi Offered By Unacademy

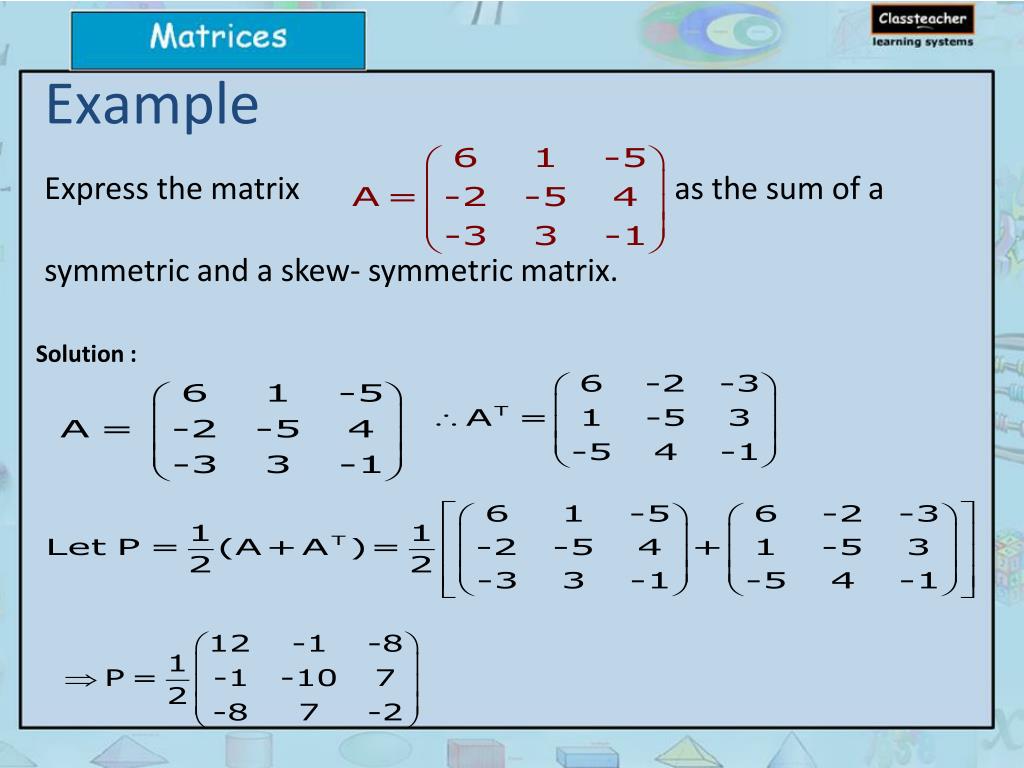
Ppt Symmetric And Skew Symmetric Matrices Powerpoint Presentation Free Download Id 2646318

Symmetric Skew Symmetric And Orthogonal Matrix Linear Algebra L2 P1 Youtube

Pdf Almost Skew Symmetric Matrices

Symmetric And Skew Symmetric Matrices Definition Theorem Solved Example Problems