Pseudo Inverse Matrix Properties
AA-1 A-1A I where I is the Identity matrix The identity matrix for the 2 x 2 matrix is given by. This article collects together a variety of proofs involving the MoorePenrose inverse.

Left Inverse And Right Matrix Inverses Youtube
Alternatively we could compute the pseudoinverse by flrst computing the SVD of A as A UVT and then by the flrst theorem of this section A VUT where S1 0 0 0.

Pseudo inverse matrix properties. A includes all real pseudo-inverse matrices A for all A2A 7. The following properties due to Penrose characterize the pseudo-inverse of a matrix and give another justification of the uniqueness of A. For any interval matrix A 2IRm n we de ne the interval pseudo-inverse matrix A 2IRn m as the minimal interval matrix so that A A.
I is identity matrix. The pseudoinverse is what is so important for example when. The nullspace of A is the nullspace of AT.
Pute the Moore-Penrose pseudoinverse of any matrix since AAT and ATA are symmet-ric. In linear algebra the MoorePenrose inverse is a matrix that satisfies some but not necessarily all of the properties of an inverse matrix. Just as the generalized inverse the pseudoinverse allows mathematicians to construct an inverse like matrix for any matrix but the pseudoinverse also yields a unique matrix.
This way A does it the other way is the pseudo-inverse and the pseudo-inverse just kills this stuff and the matrix just kills this stuff. N m A. More formally the Moore-Penrose pseudo inverse A of an m -by- n matrix is defined by the unique n -by- m matrix satisfying the following four criteria we are only considering the case where A consists of real numbers.
If m. However the Moore-Penrose pseudo inverse is defined even when A is not invertible. Suppose that A is m n real matrix.
AAA A AAA A AA AA AA AA. Pseudoinverse Orthogonal Projection Operators ECE275AStatisticalParameterEstimation KenKreutz-Delgado ECEDepartmentUCSanDiego KenKreutz-Delgado UCSanDiego ECE 275A Fall2011 148. Lemma 1113 Given any m n-matrix A real or complex the pseudo-inverse A of A is the unique nm-matrix satisfying the following properties.
So everything thats really serious here is going on in the row space and the column space and now tell me -- this is the fundamental fact that between those two r-dimensional spaces our matrix is. The inverse of a matrixAis uniqueand we denote itA1. C D T D T C T.
In this case Axbhas the solution xA-1b. Where I is the n n identity matrix then A T is invertible and its inverse is B that is B A T 1. Here A AI holds.
The theoretical definition of the pseudoinverse is given by the following conditions. Here in the first equality we used the fact about transpose matrices that. A A T A-1 A T satisfies the definition of pseudoinverse.
Properties of the pseudoinverse of a matrix. N m A T A. If Ais invertible thenA1is itself invertible andA11A.
Proofs involving the MoorePenrose inverse. If A is invertible then the Moore-Penrose pseudo inverse is equal to the matrix inverse. Im quite sure I need to use the four properties of the pseudo inverse but Im not exactly sure how.
We claim that we can take A 1 T for this B. The command is called mpp. Penrose inverse or pseudoinverse founded by two mathematicians EH.
We start from the singular value. For the cases where has full row or column rank and the inverse of the correlation matrix for with full row rank or for full column rank is already known the pseudoinverse for matrices related to can be computed by applying the ShermanMorrisonWoodbury formula to update the inverse of the correlation matrix which may need less work. Moreover I also know that in general we cannot expect A A I.
M n A T. Let A be a n m and matrix and let B A T A 1 A T be its pseudo inverse. Properties of Matrices Inverse If A is a non-singular square matrix there is an existence of n x n matrix A-1 which is called the inverse of a matrix A such that it satisfies the property.
If Ais invertible andc 0is a scalar thencAis invertible andcA11cA1. Contrary to the interval inverse matrix we. The pseudoinverse of an arbitrary-shaped matrix latex A written latex A has the same shape as latex A T and solves our problem.
The properties of the matrix will change. The pseudoinverse A of A is the matrix for which x A Ax for all x in the row space of A. Suppose that A is m n real matrix.
A T A 1 T A 1 A T I T I. The answer to both optimization methods above is given by latex x A y. Pseudoinverse The inverseA-1of a matrix Aexists only if Ais square and has full rank.
This is the way its done in Matlab. Here are the four properties that the pseudoinverse must satisfy as listed in my text. Moore in 1920 and Roger Penrose in 1955.
In fact we have. The pseudoinverseAbeware it is often denoted otherwise is a generalization of the inverse and exists for any mnmatrix. In particular if the related matrix differs from the original one by only a.
If m n and if the inverse of A T A exists. The rank of A and A is n. TheoremProperties of matrix inverse.
Inverting the Jacobian Pseudo Inverse We can try using the pseudo inverse to find a matrix that effectively inverts a nonsquare.

Introduction To The Pseudo Inverse Youtube

3 32 Prove That The Pseudoinverse A Of An M N Chegg Com
Block Matrix Pseudoinverse Wikipedia

What Is The Computational Complexity Of The Pinv Command In Matlab

Find The Least Squares Solution To The Matrix Equation Or Pseudo Inverse Youtube

Pdf Fast Computing Of The Moore Penrose Inverse Matrix
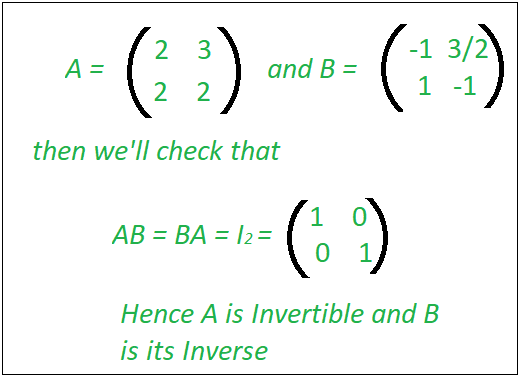
Check If A Matrix Is Invertible Geeksforgeeks

Generalized Inverse Of 2 X 2 Block Matrix Mathematics Stack Exchange

Matrix Inverse From Wolfram Mathworld

2 A Find The Pseudoinverse A Ata 1 At Of The Chegg Com

Linear Algebra For Machine Learning Part 5 Singular Value Decomposition Svd And Matrix Pseudo Inverse By Falguni Mukherjee Medium

How To Calculate The Inverse Of A Diagonal Matrix Quora

1 The Moore Penrose Pseudo Inverse

Matrix Inverse Properties Youtube

Solved 3 32 Prove That The Pseudoinverse A Of An M N M Chegg Com

Outline Properties On The Matrix Inverse Matrix Inverse Lemma Ppt Download
Can Non Square Matrices Have Inverses Quora

