How To Multiply Singular Matrix

15 Aug, 2021

18 8 1. Singular matrix and MATLAB inversion.

Identity Matrix Inverse Invertible Singular Matrix Determinant Multiply

The given matrix does not have an inverse.

How to multiply singular matrix. In order to check if the given matrix is singular or non singular we have to find the determinant of the given matrix. Has a determinant of zero. When we multiply a number by its reciprocal we get 1.

Hence the matrix is singular matrix. A is singular iff there is some xneq 0 such that Ax 0. 8 18 1.

Where A is a square symmetric matrix. If B is singular there is some xneq 0 such that Bx 0 hence AB x0 and so AB is singular. Specifically multiplying a 2x3 with a 3x2 matrix.

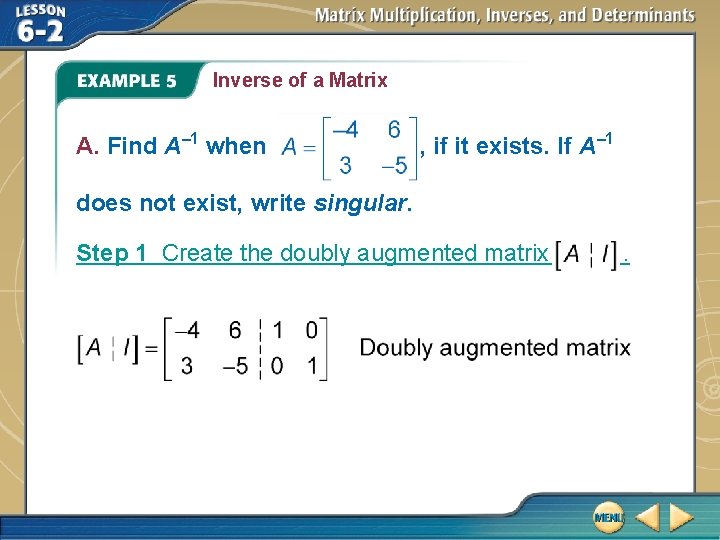
Find all values of x so that a given matrix is singular. This video covers one example of matrix multiplication. It is a singular matrix.

Hence AB is singular. To perform the rotation on a plane point with standard coordinates v x y it should be written as a column vector and multiplied by the matrix R. 1 45-48-2 36-423 32-35 1 -3 - 2 -6 3 -3 -3 12 - 9.

When we multiply a matrix by its inverse we get the Identity Matrix which is like 1 for matrices. This gives us the number we need to put in the first row first column position in the answer matrix. Find the matrix determinant the rank raise the matrix to a power find the sum and the multiplication of matrices calculate the inverse matrix.

Then det Adet B0. CAB assuming matrices are conformable for multiplication Now det Cdet AB det Adet B0. Notice that the second row is just 8x the first row.

A -1 A I. Each row is a linear combination of the first row. If B is invertible then let x B-1 x where Ax 0 then ABx Ax 0.

How come that det A 0 and yet MATLAB computes the inverse of A ie inv A is computed without any warnings. If x and y are the endpoint coordinates of a vector where x is cosine and y is sine then the above equations become the trigonometric summation angle formulae. Like Subscribe ShareIf you have a suggestion f.

Same thing when the inverse comes first. Using a property of determinants Hence C too is a singular matrix. Let A and B be 2 singular matrices and C be their product.

A A -1 I. Determinan matriks ordo 22 33 nxn dan contoh soalnya. This is the definition of a Singular matrix one for which an inverse does not exist By definition by multiplying a 1D vector by its transpose youve created a singular matrix.

We multiply the individual elements along the first row of matrix A with the corresponding elements down the first column of matrix B and add the results.

What Is A Nonsingular Matrix Quora