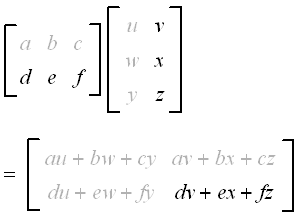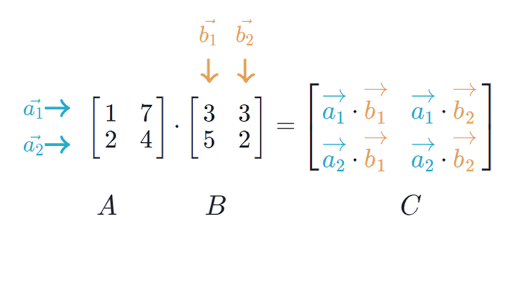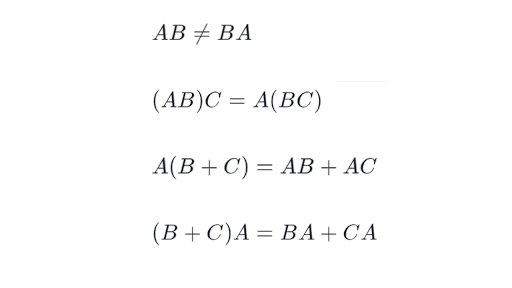Matrix Multiplication Dimension Rules
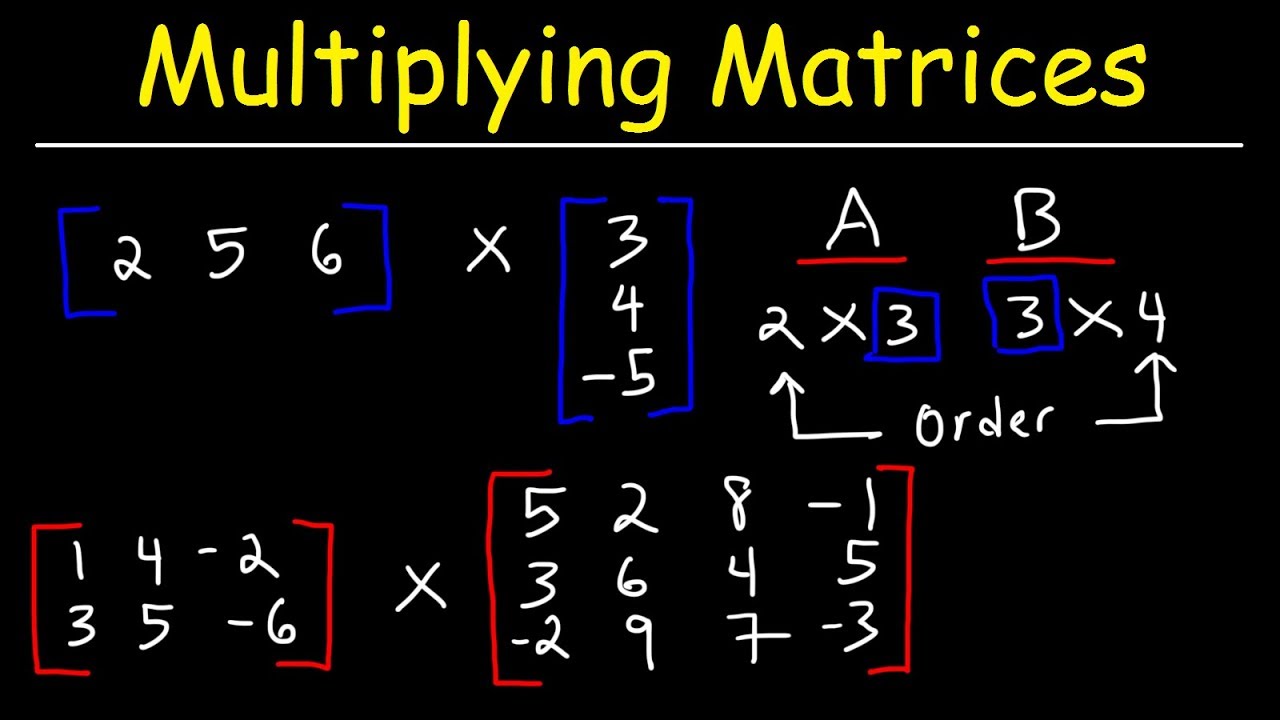
If you had matrix 1 with dimensions axb and matrix 2 with cxd then it depends on what order you multiply them. The rule for matrix multiplication however is that two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second that is the inner dimensions are the same n for an mn-matrix times an np-matrix resulting in an mp-matrix.
That is if the first matrix is m -by- 3 the second must be 3 -by- n.
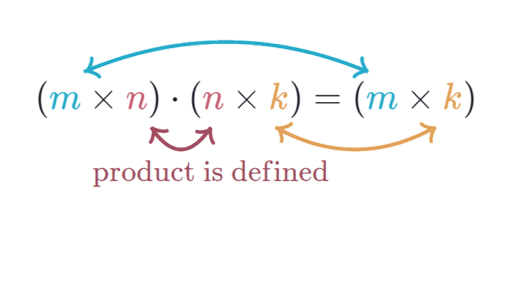
Matrix multiplication dimension rules. So if you did matrix 1 times matrix 2 then b must equal c in dimensions. The dimensions of the matrix will remain the same before and after the multiplication. In this lesson we will look at the properties of matrix scalar multiplication.
Multiplying each element in the matrix by the integer will produce the answer matrix. The integer will be distributed to each entry in the matrix by multiplication. It operates according to the rules of linear algebra.
These properties include the dimension property for scalar multiplication associative property and distributive property. Even when two matrices have dimensions allowing them. You can multiply two matrices if and only if the number of columns in the first matrix equals the number of rows in the second matrix.
In multiplying matrices it helps to remember this key rule. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. The inner dimensions must be the same.
If the first matrix has a dimension of a times b and the second matrixs dimension is m times n for matrix multiplication to be defined the number of columns of the first matrix b must equal the number of rows of the second matrix m. As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one. Kind of like subtraction where 2-3 -1 but 3-21 it changes the answer.
Here are the steps for each entry. Let us say we are multiplying three matrices A B and C and the product is D ABC. Since we multiply the rows of matrix A by the columns of matrix B the resulting matrix C will have a size of 2 x 2.
When you multiply a matrix by a integer it is called scaler multiplication. If A a i j is an m n matrix and B b i j is an n p matrix the product A B is an m p matrix. Matrix multiplication does not operate element-by-element.
Multiplication between 3 matrices Multiplication of the three matrices will be composed of two 2-matrix multiplication operations and each of the two operations will follow the same rules as discussed in the previous section. In multiplication of two n dimensional matrices starting n 2 numbers should be same and last two numbers should follow the rule of 2 d multiplication ie column of left should be equal to row of right. A b c d e a b c e f a b c d f.
The dimension property states that multiplying a scalar with a matrix call it A will give another matrix that has the same dimensions as A. MULTIPLICATION OF A MULTIDIMENSIONAL MATRIX BY A SCALAR Multiplication of a multidimensional matrix by a scalar results in multiplying every element of the multidimensional matrix by the scalar. In the following example a 4-D matrix with dimensions of.
Now the rules for matrix multiplication say that entry ij of matrix C is the dot product of row i in matrix A and column j in matrix B. 24 28 22 48 4 32 36. The resulting matrix will have a dimension equal to the number of rows of the 1st matrix and the number of columns of the 2nd matrix.
Link on columns vs rows In the picture above the matrices can be multiplied since the number of columns in the 1st one matrix A equals the number of rows in the 2 nd matrix B. You can only multiply two matrices if their dimensions are compatible which means the number of columns in the first matrix is the same as the number of rows in the second matrix. To multiply matrices they need to be in a certain order.
Or more generally the matrix product has the same number of rows as matrix A and the same number of columns as matrix B. We can use this information to find every entry of matrix C.
Matrix Multiplication Dimensions Article Khan Academy

Understanding Affine Transformations With Matrix Mathematics Matrices Math Mathematics Matrix Multiplication

Matrices Matrix Operations About Matrices A Matrix Is
Matrix Multiplication Made Easy
Multiplying Matrices Article Matrices Khan Academy

Matrix Multiplication In C Javatpoint
Matrix Multiplication Made Easy
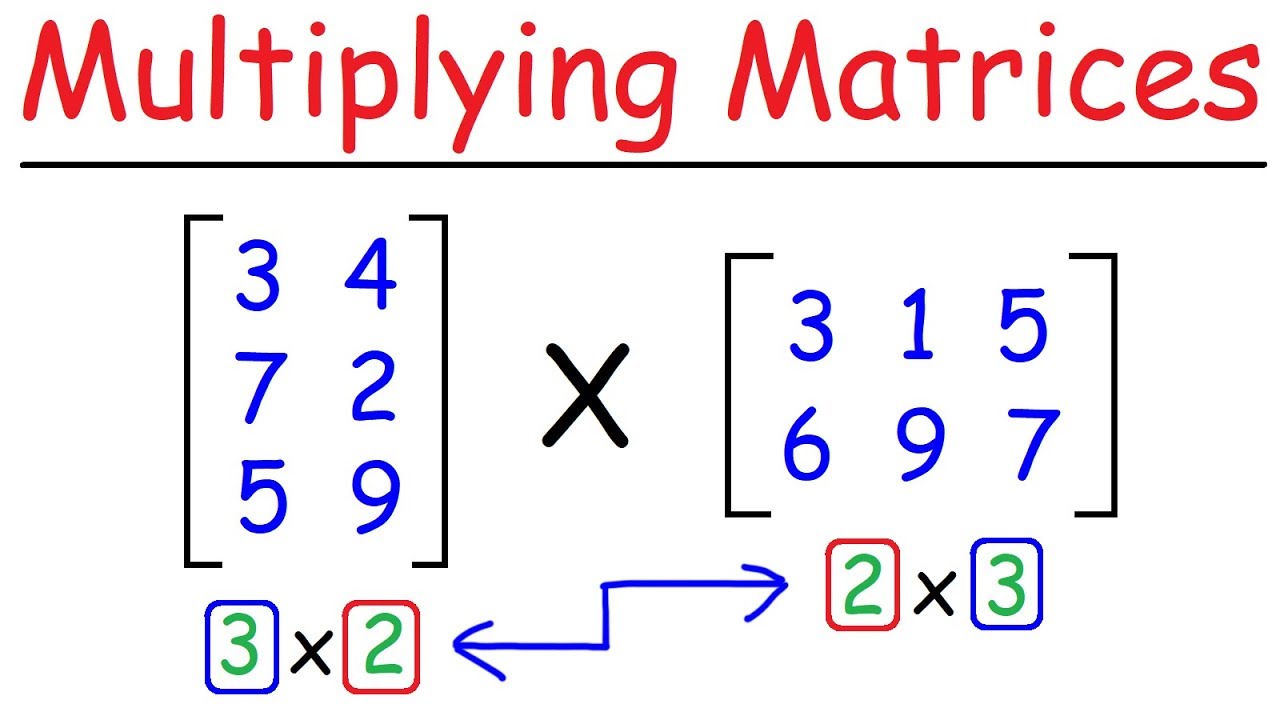
How To Multiply Matrices Quick Easy Youtube

Pin On Math Classroom Activities
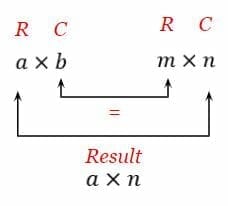
Matrix Multiplication Explanation Examples
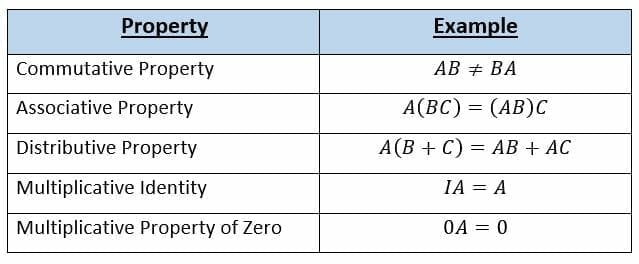
Properties Of Matrix Multiplication Article Khan Academy
Matrix Multiplication Dimensions Article Khan Academy

3 4a Matrix Operations Finite Math

How To Multiply Matrices Quick Easy Youtube
Matrix Multiplication Explanation Examples