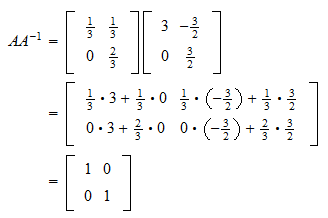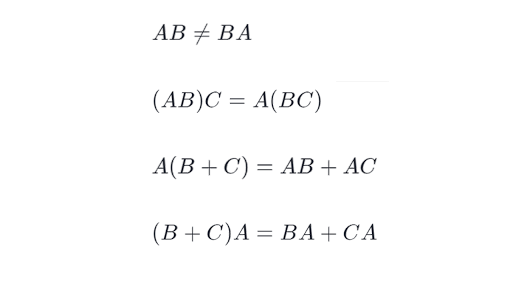Matrix Multiplication Proof Inverse
1 4 А -2 b. If Ais invertible thenA1is itself invertible andA11A.
Square matrix has an inverse.
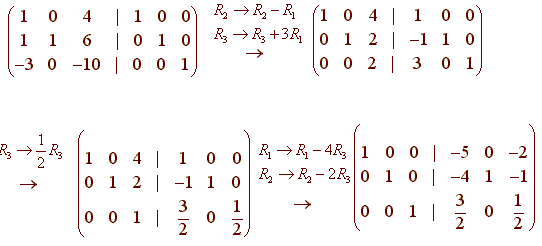
Matrix multiplication proof inverse. So to check whether a matrix B really isthe inverse of A you multiply B by A in both orders any see whether. I suggest proving it in one line. You may want to use the row or column method of matrix multiplication to justify your answer.
The formula used in this video. Since Multiplying matrices is associative. If A is a non-singular square matrix there is an existence of n x n matrix A-1 which is called the inverse of a matrix A such that it satisfies the property.
А 12 -17 PC-2 21 where pa z221 C. Commutativity is not true. AA-1 A-1A I where I is the Identity matrix The identity matrix for the 2 x 2 matrix is given by.
Xrightarrow X is injective then fx Lx as above has an inverse g that is defined everywhere on X which forces fcirc gyy for all y in Y. Zero matrix on multiplication If AB O then A O B O is possible 3. The rule for computing the inverse of a.
Find A-1 by guess and check. If it does then A1 A I AA1 and we say that A is invertible or nonsingular. 11 11 A A 12 A 21 A 22 22 jA jjF 11j jA jjF 22j 9a A 11 A 12 A 21 A 22.
AB BA 2. Let Binmathbb Fntimes n be right inverse Cinmathbb Fntimes n left inverse of Ainmathbb Fntimes n. TheoremProperties of matrix inverse.
AB C A BC 4. You can then consider c to be the n n matrix c I d so that every entry in the diagonal equals c and 0 everywhere else and where A is also n n and then c I d is invertible for all c 0 and then apply the result that the inverse of A B is B 1 A 1. I therefore wanted to go back and try to prove various claims.
If A is singular ie. If Ais invertible andc 0is a scalar thencAis invertible andcA11cA1. BIBCABCABCABCIC Thus BC as required.
A does not have an inverse its determinant is zero and we can find some non-zero vector x for which Ax 0. For conformably partitioned block matrices addition and multiplication is performed by adding and multiplying blocks in exactly the same way as scalar elements of regular matrices however determinants and inverses of block matrices are very tricky. A matrix B is the inverse of a matrix A if it has the propertythat multiplying B by A in both orders gives the identity I.
If there exists a matrix B also n n such that AB BA I n then B is called the multiplicative inverse of A. Denition 77 Let A be an n n matrix. The multiplicative inverse of a matrix A is usually denoted A 1.
Clearly any Kronecker product that involves a zero matrix ie a matrix whose entries are all zeros gives a zero matrix as a result. For 2 blocks by 2 blocks the results are. In other words if M is a matrix such that MLI on the finite dimensional linear.
For each matrix either provide an inverse or show the matrix is not invertible. For a square matrix A AI IA A. Again by applying the definition of Kronecker product and that of multiplication of a matrix by a scalar we obtain Zero matrices.
Lets look at some properties of multiplication of matrices. This also came up in exercise 1424 as well which I answered without necessarily fully understanding the problem. Each A below is invertible.
In this video were going to be looking at a general view on how to use Excel for Matrix equations in a step by step process. If A is a square matrix the most important question you can ask about it is whether it has an inverse A1. Therefore if L.
Then CnOnomega2Cn2 You can solve this recurrence and get CnOnomega using Master theorem. Multiplying a matrix A by a constant c is the same as scaling every row of a matrix by c. Write Cn the complexity of inversion of ntimes n matrix and omega the matrix multiplication complexity exponent.
We begin with the denition of the inverse of a matrix. A B C AB AC A B C AC BC 5. In doing exercise 1610 in Linear Algebra and Its Applications I was reminded of the general issue of multiplying block matrices including diagonal block matrices.
The inverse of a matrixAis uniqueand we denote itA1. 1 007 A0 0 1 10 a.

Inverses Of Matrices And Its Properties Mathematics Stack Exchange
How To Prove The Inverse Of The Matrix Quora

Linear Algebra Chapter 2 Matrices Ppt Video Online Download

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube

Verify That Two Matrices Are Inverses Youtube

Prove That The Order Of Multiplication For Two Square Matrices Whose Product Is Equal To The Identity Matrix Does Not Matter Mathematics Stack Exchange

Properties Of Inverses Of Matrices Definition Theorem Formulas Solved Example Problems Inverse Of A Non Singular Square Matrix

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download

Matrix Inverse Properties Youtube
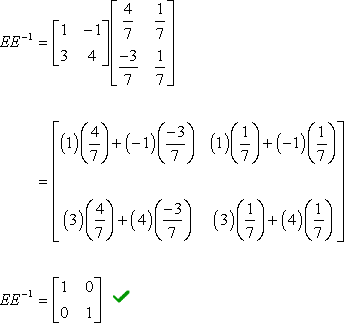
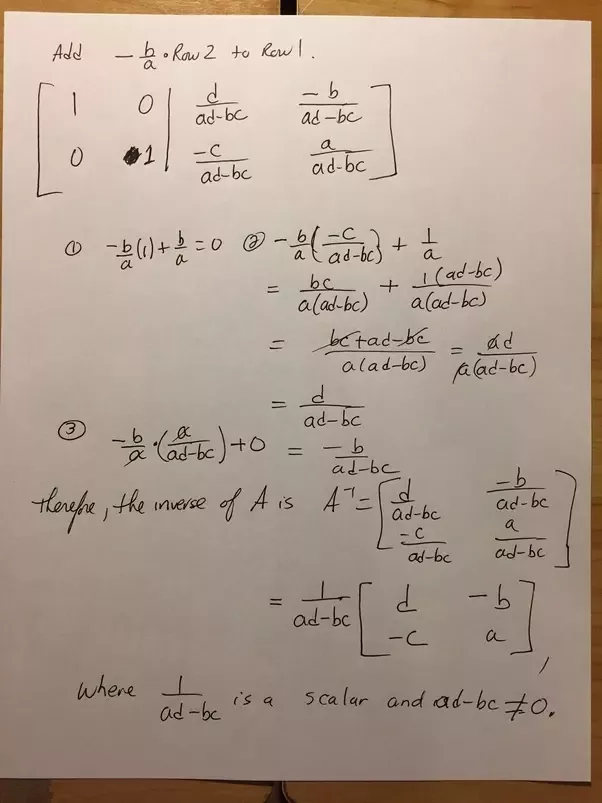
Inverse Of A 2x2 Matrix Chilimath

Find The Multiplicative Inverse Of A Matrix Youtube

Linear Algebra 85 Inverse Of A Matrix Proof Youtube

How To Prove The Inverse Of The Matrix Quora
Properties Of Matrix Multiplication Article Khan Academy

Inverse Of A Matrix Advanced Higher Maths

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download

Are Two Matrices Inverses Of Each Other Youtube

Inverses And Elementary Matrices