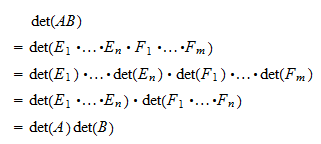Product Of Diagonal Elements Of Matrix Determinant
Lets say I have a matrix where everything below the main diagonal is a zero and Ill start just for the sake of argument lets start with a 2x2 matrix so lets start with a 2x2 matrix so I have the values a B 0 and D so instead of a C I have a 0 there so everything below and the main diagonal is a 0 so what is the determinant of this going to be lets call that matrix a so the determinant of. B A AB.

Ex 2 Determinant Of 3x3 Matrix Diagonal Method Youtube
A diagonal matrix is sometimes called a scaling matrix since matrix multiplication with it results in changing scale size.
Product of diagonal elements of matrix determinant. For the case of a 2 2 matrix let A a 11 a 12 0 a 22. Combination If Eis an elementary matrix for a combination rule then detEA detA. The determinant of a matrix is zero if all the elements of the matrix are zero.
The determinant of an upper triangular matrix is the product of its diagonal elements. Find the determinant of a diagonal matrix. Then property 3 a tells us that the determinant of this diagonal matrix is the product d1d2 dn times the determinant of the identity matrix.
For calculation of inverse matrix we know all these many efficient algorithms. Laplaces Formula and the Adjugate Matrix Apart from these properties of determinants there are some other properties such as. In general only when the matrix is a triangular or diagonal matrix the product of the elements of the diagonal will be equals to the determinant of.
Swap If E is an elementary matrix for a swap rule then detEA 1detA. This is a one-arrow Sarrus rule valid for dimension n. The final result determinant of the given matrix is equal to minus 1.
DetA a 11a 22 a nn. So det A a 11 a 22 and the statement is true for the case of a 2 2 matrix. In a triangular matrix the determinant is equal to the product of the diagonal elements.
Where J is a matrix with all elements equal to 1 and D is a diagonal matrix with all elements greater than 1 since in the original matrix the diagonal is positive. Whenever or alternatively whenever. Prove that the determinant of an upper triangular matrix is the product of its diagonal entries.
We will prove this by induction for an n n matrix. DetA a11a22 ann. An identity matrix of any size or any multiple of it a scalar matrix is a diagonal matrix.
One can transform a given matrix to a triangular form and then compute its determinant with the help of property 5. First repeat after me. The determinant of the product of two square matrices is equal to the product of their determinants.
Since its a diagonal expanding along the first row will give you the fi. See full answer below. If is a triangular matrix ie.
Since elementary row operations do not alter the determinant of a matrix the required determinant is the product of the diagonal elements of the transformed matrix. An example is not a proof. The properties can be used to calculate determinants.
Triangular matrix Ais the product of the diagonal elements. Its determinant is the product of its diagonal values. Property 5 tells us that the determinant of the triangular matrix wont change if we use elimination to convert it to a diagonal matrix with the entries di on its diagonal.
Thisis a one-arrow Sarrus rule valid for dimensionnIfEis an elementary matrix for a swap rule thendetEA 1 detA. Become a member and. The rules can be The value of detAfor either an upper triangularor a lower triangular matrixAis the product of thediagonal elements.
The determinant of upper triangular matrix is equal to the product of the diagonal elements of this matrix which is 1. Property 1 completes the argument. Note that the matrix J can be written as an outer product between two vectors with all entries equal to 1 J 1 1 T.
However if you do a few examples you can use them as scaffolding for a proof.

Let A And B Benxn Matrices Mark Each Statement True Chegg Com

The Determinant Of A Triangular Matrix Is The Product Chegg Com
Are The Following Statement True Or False The Chegg Com
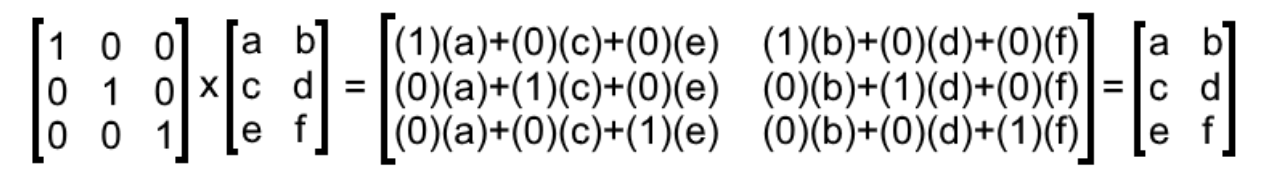
What Is An Identity Matrix Studypug

If Product Of Two Nonzero Matrix Matrices Is Zero Matrix Then They Are Singular Matrices Youtube

Introduction To Matrices Boundless Algebra

Lesson Video Properties Of Determinants Nagwa
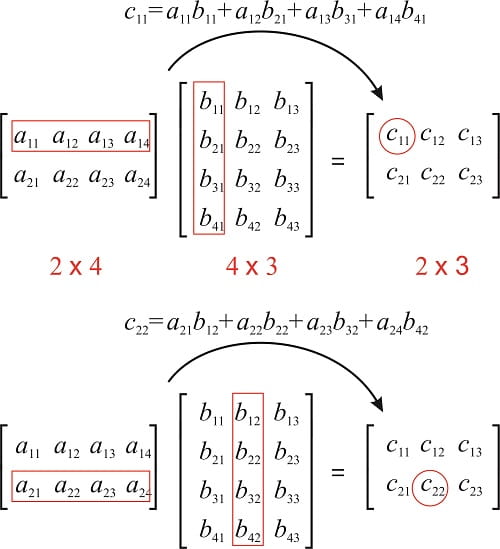
02 00 Linear Algebra Ipynb Colaboratory
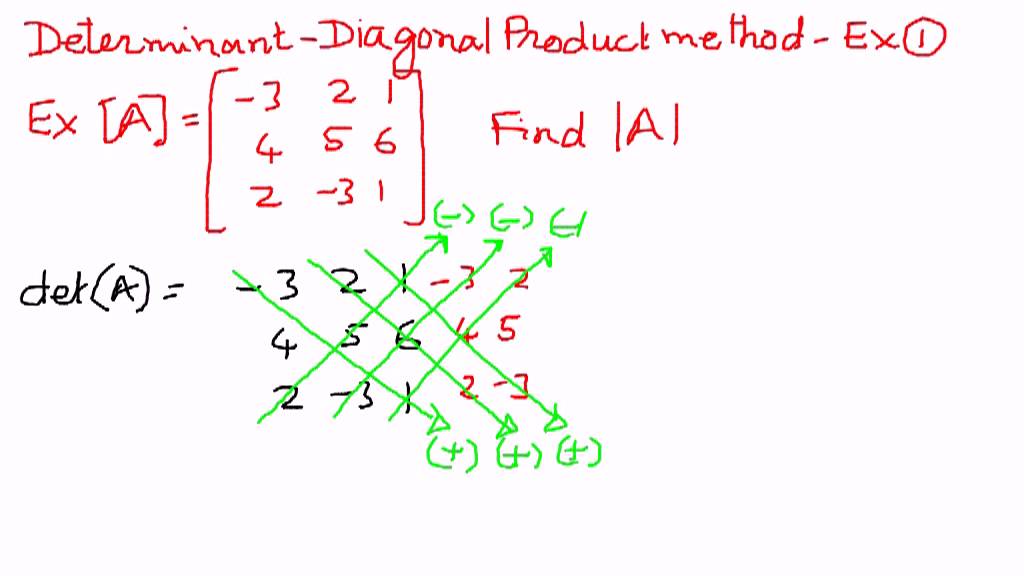
Determinants Diagonal Product Method Example 1 Youtube

A Show That The Product Of Two 2 X 2 Upper Chegg Com
For A Symmetric Matrix With Different Diagonal Elements Is There A Shortcut Method Other Than The Conventional One To Find Its Determinant Quora

Matrix Matrices An Overview Sciencedirect Topics

The Determinant Of A 3 X 3 Matrix General Shortcut Method Studypug

Question Video Solving Equations By Finding The Determinant Of A Diagonal Matrix Nagwa

Diagonal Matrix Definition Examples And Its Properties

F If A Is An N X N Matrix Then The Determinant Of Chegg Com

Upper Triangular Determinant Video Khan Academy