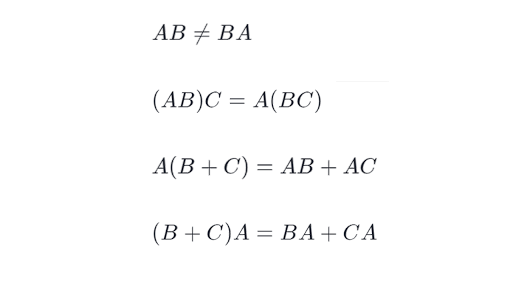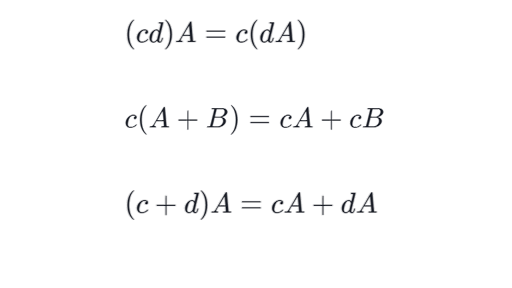Is Matrix Transpose Distributive
MathABT AT BT. Let B and C be n r matrices.

Transpose Of A Matrix Definition Properties Videos And Solved Examples
Given an mn matrix A its transpose AT is the nm matrix defined by aT ij aji.

Is matrix transpose distributive. That is given a matrix A A 0 0 A A. Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. The matrix I is the identity of matrix multiplica.
The transpose of a transposed matrix is equal to the original matrix. Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. The conjugate transpose of a matrix with real entries reduces to the transpose of as the conjugate of a real number is the number itself.
E A I 1 A n n. 0 0 0 0. For every square matrix A there exists an identity matrix of the same order such that IA AI A.
Further 0A A0 0 where 0 is the appropriately sized 0 matrix. Adding two matrices and then transposing the result is the same as transposing each matrix first and then adding them. So if AAAAIIdentity matrix then A is called an Orthogonal Matrix.
Transpose of a Matrix. A BC AB C fulfills associative law. The matrix 0 is the identity of matrix addition.
1 1 1 1. So for now lets talk about the characteristics of the Transpose matrix. Which does not require distributuivity of transpose it is just exponentiation of an arbitrary matrix.
Find the transpose of the matrix and verify that A T T A. He A matrix in this equation is called the coefficient matrix for the system. The Distributive Property of Matrices states.
Because before entering that we have to know some more things. Find AB C and AB AC. Distributive law for rows Suppose that matrices XYZ are identical except for the ith row and the ith row of Z is the.
Given a matrix A the transpose of A denoted AT is the matrix whose rows are columns. AB T B T A T The same is true for the product of multiple matrices. E A T I 1 A T n n.
The conjugate transpose can be motivated by noting that complex numbers can be usefully represented by 22 real matrices obeying matrix addition and. Some laws on matrix multiplication. Transpose of a matrix Definition.
Note that it is possible to have two non-zero ma-trices which multiply to 0. AB C AB AC. Now we talk later about orthonormal vectors and all.
1 1 1 1 1 1 1 1. E A T I 1 A T n n. Basically we are flipping it along its main diagonal consisting of the elements aii.
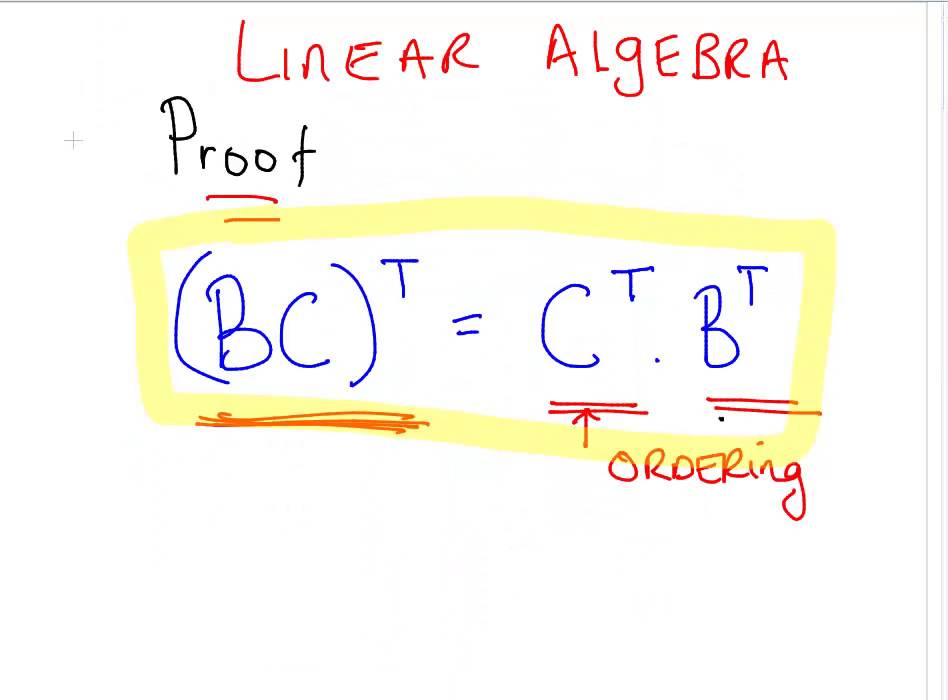
The transpose of the product of two matrices is equivalent to the product of their transposes in reversed order. You want to prove an equality of matrices. The transpose of A is the matrix whose entry is given by Proposition.
A BC AC BC cAB cAB AcB where c is a constant please notice that AB BA Multiplicative Identity. Non-commutative multiplication AB BA. So for all mathimath and mathj.
Verify the associative property of matrix. If A and B are the transpose of the matrices A and B then 1. Also if A be an m n matrix and B and C be n m matrices then.
Tagmath The crucial thing to remember is that two matrices are equal if and only if all of their corresponding entries are equal. And use distributivity of transpose and A n T A T N to write. A B C AB AC B C A BA CA fulfills distributive law.
Transpose of a matrix. B CA BA CA. Let A be an matrix.
A 1 2 0 1 B 0 1 1 1 C 2 0 0 1. Ie AT ij A ji ij. If A B C matrix meet the required matrix multiplication requirements then.
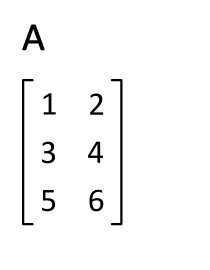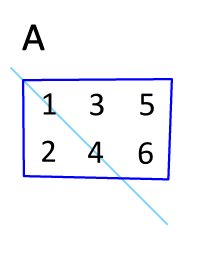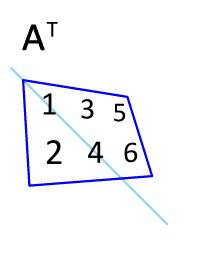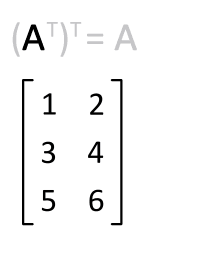
By definition of matrix multiplication and the identity matrix Using the lemma I proved on the Kronecker delta I get Thus and so. 85 Transpose of a Matrix A matrix can be transformed by transposing it. In other words we interchange rows and columns to transpose the matrix.
They are the only matrices that have inverses as same as their transpositions. ABC T C T B T A T. Example 4 1 1 1 1.
The transpose of a matrix has the following characteristics. Let A and B be matrices of the same dimension and let k be a number. Transpose of a product.
A matrix has an inverse if and only if it is both squares as well as non-degenerate. And the transpose of the transpose matrix. Moreover the inverse of an orthogonal matrix is referred to as its transpose.
Thus this inverse is unique. Let A be an m n matrix. The transpose of matrix A is determined as shown below.

Section 1 4 Inverses Rules Of Matrix Arithmetic Ppt Download

Linear Algebra 63 Properties Of Matrix Transpose Proofs Youtube

Matrices Introduction Lecture 1 3 Online Presentation

Linear Algebra 57 Matrix Multiplication Properties And Proof Youtube
A Hackers Guide To Deep Learning S Secret Sauces Linear Algebra By Leon Fedden Medium
Properties Of Matrix Multiplication Article Khan Academy

Transpose Of A Matrix Definition Properties Videos And Solved Examples
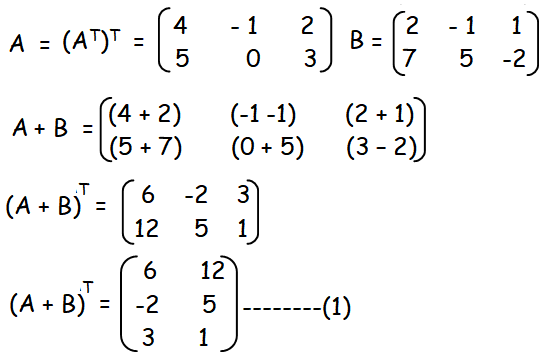
Practice Questions On Transpose Of Matrix

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download
Lesson Explainer Transpose Of A Matrix Nagwa

7 1 Matrices Vectors Addition And Scalar Multiplication

Chapter 2 Matrices 2 1 Operations With Matrices
Linear Algebra Transpose Matrices Proof Youtube

Properties Of Matrix Operations 2010 14 Sep Ki Seung Lee Ppt Download

Ppt Chapter 2 Matrices Powerpoint Presentation Free Download Id 1568385
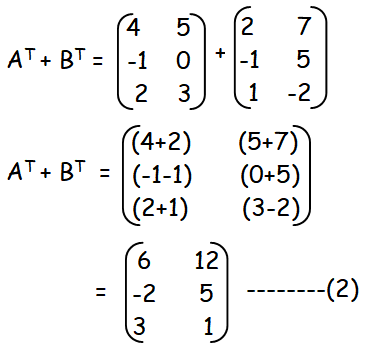
Practice Questions On Transpose Of Matrix
Properties Of Matrix Scalar Multiplication Article Khan Academy

Modified Gary Larson Far Side Cartoon Ppt Download

Table 7 3 From Matrix Algebra For Mds 7 1 Elementary Matrix Operations Semantic Scholar