Matrix Invertible Solutions

Inverse Matrix Calculator usually adopts Gauss-Jordan also known as Elementary Row Operations method and Adjoint method to perform the intended function. 1 007 A0 0 1 10 a.

Singular Matrix Video Lessons Examples And Solutions

As a result you will get the inverse calculated on the right.

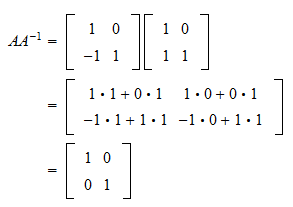
Matrix invertible solutions. Find A-1 by guess and check. Ax b is consistent for all b in R n. So the equation has a solution in this case.

Inverse of a Matrix Formula Let be the 2 x 2 matrix. If this is thecase then the matrix B is uniquely determined by A and is called the inverse of A denoted by A1. This website uses cookies to ensure you get the best experience.

To find the inverse of A using column operations write A IA and apply column operations sequentially till I AB is obtained where B is the inverse matrix of A. Yes to examine the size of the solution set of a system of linear equations we look at the rank of the coefficient matrix compared with the rank of the augmented matrix. А 12 -17 PC-2 21 where pa z221 C.

Each A below is invertible. 1 4 А -2 b. Free matrix inverse calculator - calculate matrix inverse step-by-step.

If C is 66 matrix and the equation Cxv is consistent for every v in set of real numbers ℝ6 is it possible that for some v the equation Cxv has more than one solution. The matrix is right invertible. Suppose mathAmath is invertible.

Set the matrix must be square and append the identity matrix of the same dimension to it. It follows fromthe theory of matrices that if for finite square matrices A and B then also. Then mathAxb implies A-1AxA-1b implies Ix b implies x bmath.

Inverse Matrix Calculator is a mathematical tool that performs all the lengthy and tricky calculations in seconds to find the Inverse of a given Matrix. To solve a system of linear equations using an inverse matrix let latexAlatex be the coefficient matrix let latexXlatex be the variable matrix and let latexBlatex be the constant matrix. The inverse of a Matrix Suppose A is a square matrix now this A matrix is known as invertible only in one condition if their another matrix B of the same dimension exists such that AB BA I n where I n is known as identity matrix of the same order and.

Therefore the columns of A1 are linearly independent. 1 2 1 2 5 4 x 11 x 21 x 31 3 5 to get the first column of the matrix X and. Thus we want to solve a system latexAXBlatex.

This suggests a deep connection between the invertibility of A and the nature of the linear system Ax b. In other words youre solving the two linear systems. The reduced row echelon form of A is the identity matrix I n.

You may want to use the row or column method of matrix multiplication to justify your answer. To establish uniqueness suppose matha_1math and matha_2math be two solut. The columns of A form a basis for R n.

Start your free trial. According to the Invertible Matrix Theorem if a matrix is invertible its columns form a linearly independent set. All right inverses of the matrix are x1xTxRtaking all possiblevalues ofxwe get all possible right inverses.

There are several methods and shortcuts to find the inverse of a Matrix. Get step-by-step solutions from expert tutors as fast as 15-30 minutes. A X A x 1 A x 2 B.

If it is left invertible it is invertible and its right inverseis unique and coincide with the inverse. The matrix B on the RHS is the inverse of matrix A. They are all simple restatements of conditions in the invertible matrix theorem.

Abelian group augmented matrix basis basis for a vector space characteristic polynomial commutative ring determinant determinant of a matrix diagonalization diagonal matrix eigenvalue eigenvector elementary row operations exam finite group group group homomorphism group theory homomorphism ideal inverse matrix invertible matrix kernel linear. Where In denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplication. Ax 0 has no solutions other than the trivial one.

For each matrix either provide an inverse or show the matrix is not invertible. Reduce the left matrix to row echelon form using elementary row operations for the whole matrix including the right one. Your first 5 questions are on us.

Col A R n. 1 2 1 2 5 4 x 12 x 22 x 32 1 4 to get the second column of the matrix X. But we have more than.

To calculate inverse matrix you need to do the following steps. Nullity A 0. The Invertible Matrix Theorem Earlier we saw that if a matrix A is invertible then Ax b has a unique solution for any b.

What Is An Inverse Matrix Mathbootcamps

Pin On Maths

What Is An Inverse Matrix Mathbootcamps

Pin On Category Theory

Invertible Matrix Theorem Youtube

Linear Algebra Ch 2 Determinants 23 Of 48 Non Invertible Matrix Example Youtube

Finding Inverse Of A Matrix Using Formula

Finding The Inverse Of A 2x2 Matrix Examples

Inverse Matrices And Their Properties Youtube

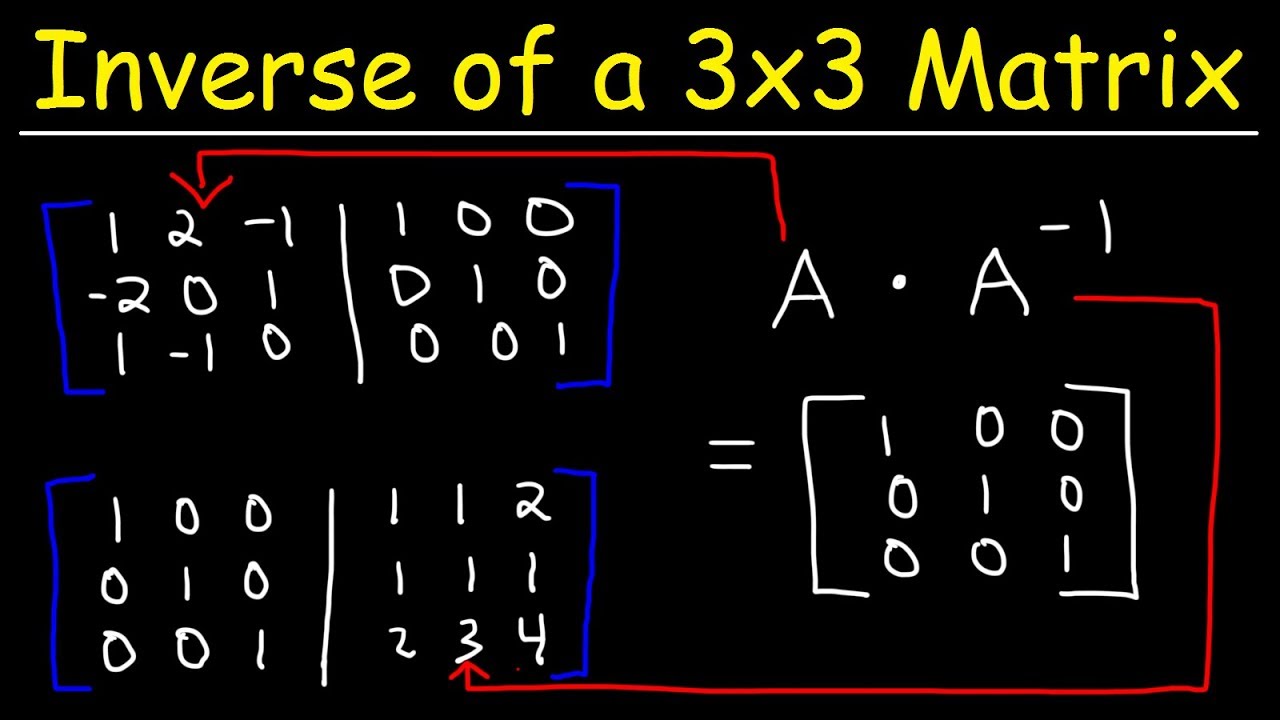
Inverse Of A 2x2 Matrix Youtube

Pin On Math Videos

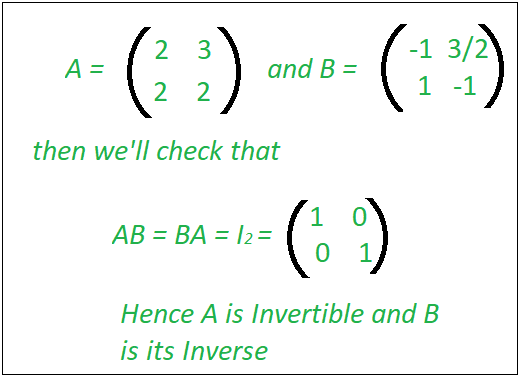
Check If A Matrix Is Invertible Geeksforgeeks

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube

Linear Algebra Cheat Sheet By Spoopyy Http Www Cheatography Com Spoopyy Cheat Sheets Linear Algebra Cheatsheet Algebra Cheat Sheet Algebra Math Cheat Sheet

Class 12th Maths Chapter 3 Matrices Part 1 All Basics Uses Of Matrix By Aman Youtube Class 12 Maths 12th Maths Teaching Mathematics

Fabric Book Weight Fuchsia Black White Gray Fabric Book Moms Crafts Fabric

Class 12th Maths Chapter 3 Matrices Part 1 All Basics Uses Of Matrix By Aman Youtube Class 12 Maths 12th Maths Teaching Mathematics

Pin On Linear Algebra Videos

Inverse Matrix