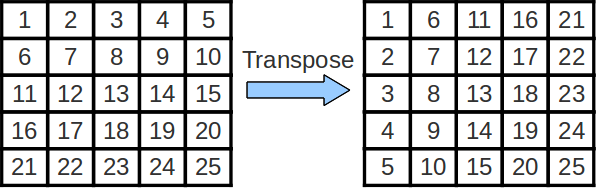
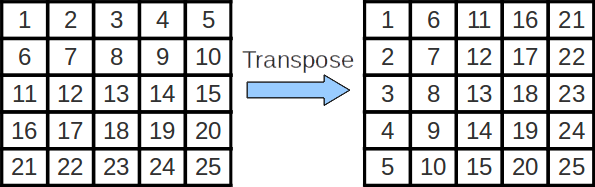
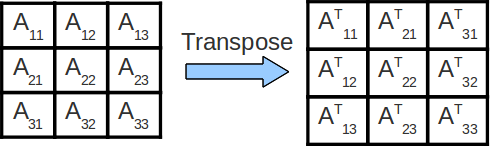
Matrix Multiplication Cache Blocking
As such we are constantly accessing new values from memory and obtain very little reuse of cached data. In the above code for matrix multiplication note that we are striding across the entire A and B matrices to compute a single value of C.

3 Blocking Tiling Optimization The Given Matrix Chegg Com
Blocked tiled matrix multiply.

Matrix multiplication cache blocking. With a total of three levels of blocking for the register file for the L1 cache and the L2 cache the code will minimize the required bandwidth at each level of the memory hierarchy. Likely to have Ob misses. Next we will analyze the memory accesses as we did before.
Searching for thrashing matrix multiplication in Google yields more results. Matrix Multiplication as an Example. My last matrix multiply I Good compiler Intel C compiler with hints involving aliasing loop unrolling and target architecture.
Typically an algorithm that refers to individual elements is replaced by one that operates on subarrays of data which are called blocks in the matrix computing field. J reads block at Cij into cache. Matrix Multiply blocked or tiled Consider ABC to be N by N matrices of b by b subblocks where bnN is called the blocksize for i 1 to N for j 1 to N read block Cij into fast memory for k 1 to N read block Aik into fast memory read block Bkj into fast memory Cij Cij Aik Bkj do a matrix multiply on blocks.
Blocked Matrix Multiplication One commonly used strategy is tiling matrices into small blocks that can be fitted into the cache. Looped over various size parameters. In this video well start out talking about cache lines.
One for each row in the block for k 0. 2 A Blocked Version of Matrix Multiply Blocking a matrix multiply routine works by partitioning the matrices into submatrices and then exploiting the mathematical fact that these submatrices can be manipulated just like scalars. To enhance the cache performance if it is not big enough we use an optimization technique.
12 April 1 Introduction In this assignment you will write code to multiply two square n n matrices of single precision floating point numbers and then optimize the code to exploit a memory cache. In your second code block ci j s but it seems that j is not declared. To achieve the necessary reuse of data in local memory researchers have developed many new methods for computation involving matrices and other data arrays 6 7 16.
Blocked Matrix Multiplication. Speeding up the multiplication of huge matrices is imperative Blocking reduces the cache misses choosing the block size is not the only optimization This paper analyzes the impact of various block size M x K and K x N on the performance. Split result matrix C into blocks C IJ of size N b x N b each blocks is constructed into a continuous array C b which is then copied back into the right C IJ.
When implementing the above we can expand the inner most block matrix multiplication Aii kk Bkk jj and write it in terms of element multiplications. Unfortunately the extra levels of blocking will incur still more loop overhead which for some problem sizes on some hardware may be more time-consuming than any shortcomings in the hardwares ability to stream data from the L2 cache. Cxxtx yyty by the NumPy notation can be computed by the corresponding rows of A and columns of B.
The major difference from an unblocked matrix multiplication is that we can no longer hold a whole row of A in fast memory because of blocking. The block method for this matrix product consist of. Blocked Tiled Matrix Multiply Consider ABC to be N-by-N matrices of b-by-b subblocks where bn N is called the block size for i 1 to Nfor j 1 to N for k 1 to N Cij Cij Aik Bkj do a matrix multiply on blocks.
If the matrices are smaller the blocked code can be slower The result is a gap between performance realized by compiled code and the achievable performance Performance Gap in Compiled. Then we can partition each matrix. Matrix Multiplication and Cache Friendly Code COMP 273 Winter 2021 Assignment 4 Prof.
The cache miss rate of recursive matrix multiplication is the same as that of a tiled iterative version but unlike that algorithm the recursive algorithm is cache-oblivious. The math behind it is that a block of C eg. I intend to multiply 2 matrices using the cache-friendly method that would lead to less number of misses I found out that this can be done with a cache friendly transpose function.
Different parameter values for K predefined values of the parameters M and N. There is no tuning parameter required to get optimal cache performance and it behaves well in a multiprogramming environment where cache sizes are effectively dynamic due to other processes taking up cache space. I L1 cache blocking I Copy optimization to aligned memory I Small 8 8 8 matrix-matrix multiply kernel found by automated search.
After that we look at a technique called blocking. Consider A B C to be NxX matrices of bxb sub-blocks where bnN is the block-size. This is where we split a large problem into small.
In the case of matrix transposition we consider performing the transposition one block at a time. 24 March Due date. More formally cache blocking is a technique that attempts to reduce the cache miss rate by improving the temporal andor spatial locality of memory accesses.
While loop unrolling safe for most matrix sizes blocking is appropriate only for large matrices eg dont block for cache for 4x4 or 16x16 matrices. For example suppose we want to compute C AB where A B and C are each 88 matrices. I for j 0.
For i 0. We can improve the amount of data reuse in the caches by implementing a technique called cache blocking.
Best Block Size Value For Block Matrix Matrix Multiplication Stack Overflow

Fast Matrix Multiplication Cache Usage Ppt Download

Fast Matrix Multiplication Cache Usage Ppt Download

Performance X64 Cache Blocking Matrix Blocking Youtube
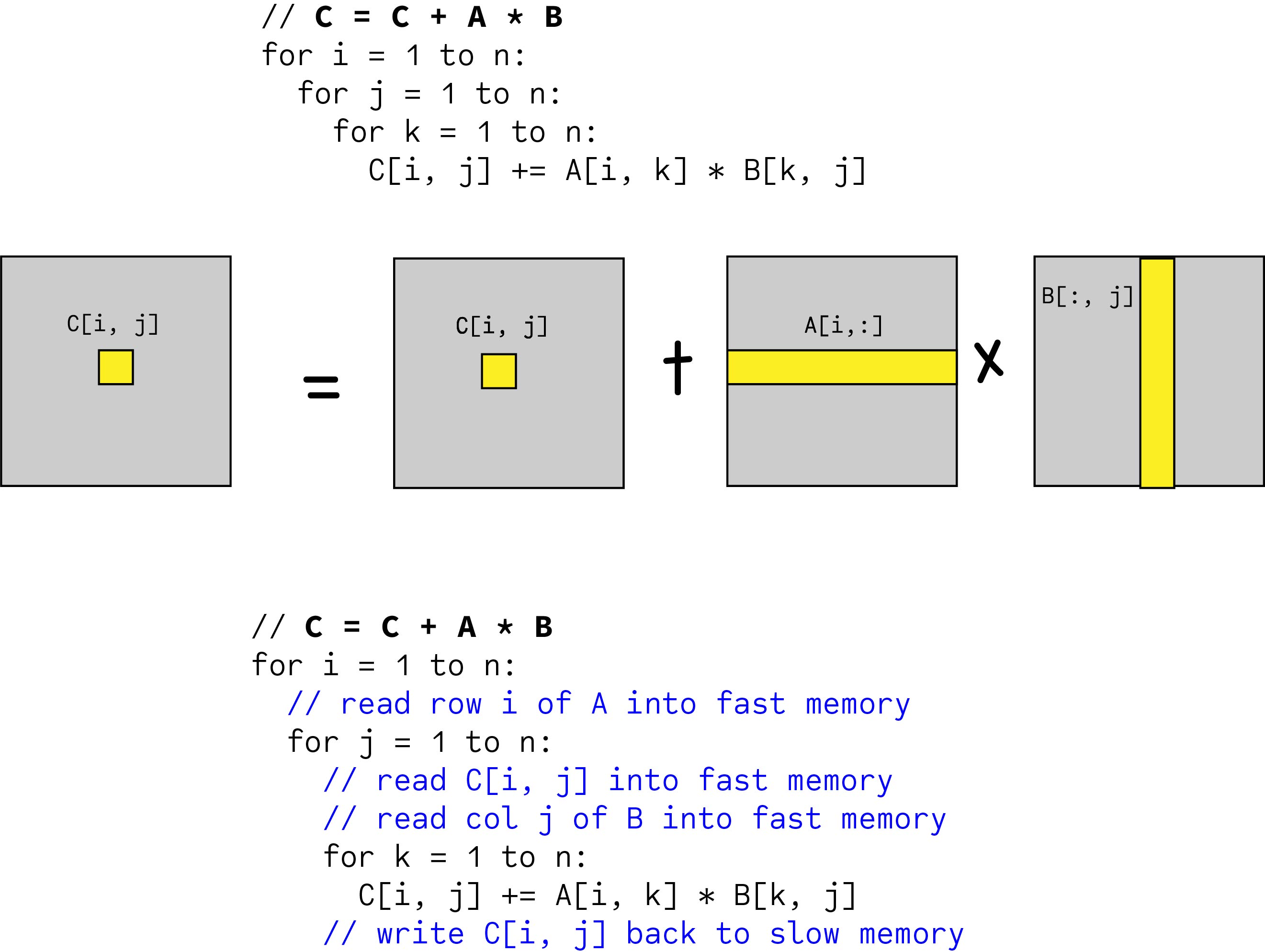
Blocked Matrix Multiplication Malith Jayaweera

Blocked Matrix Multiplication Malith Jayaweera
4 Matrix Multiplication Dive Into Deep Learning Compiler 0 1 Documentation

Block Decomposition For The Matrix Multiplication Problem Download Scientific Diagram
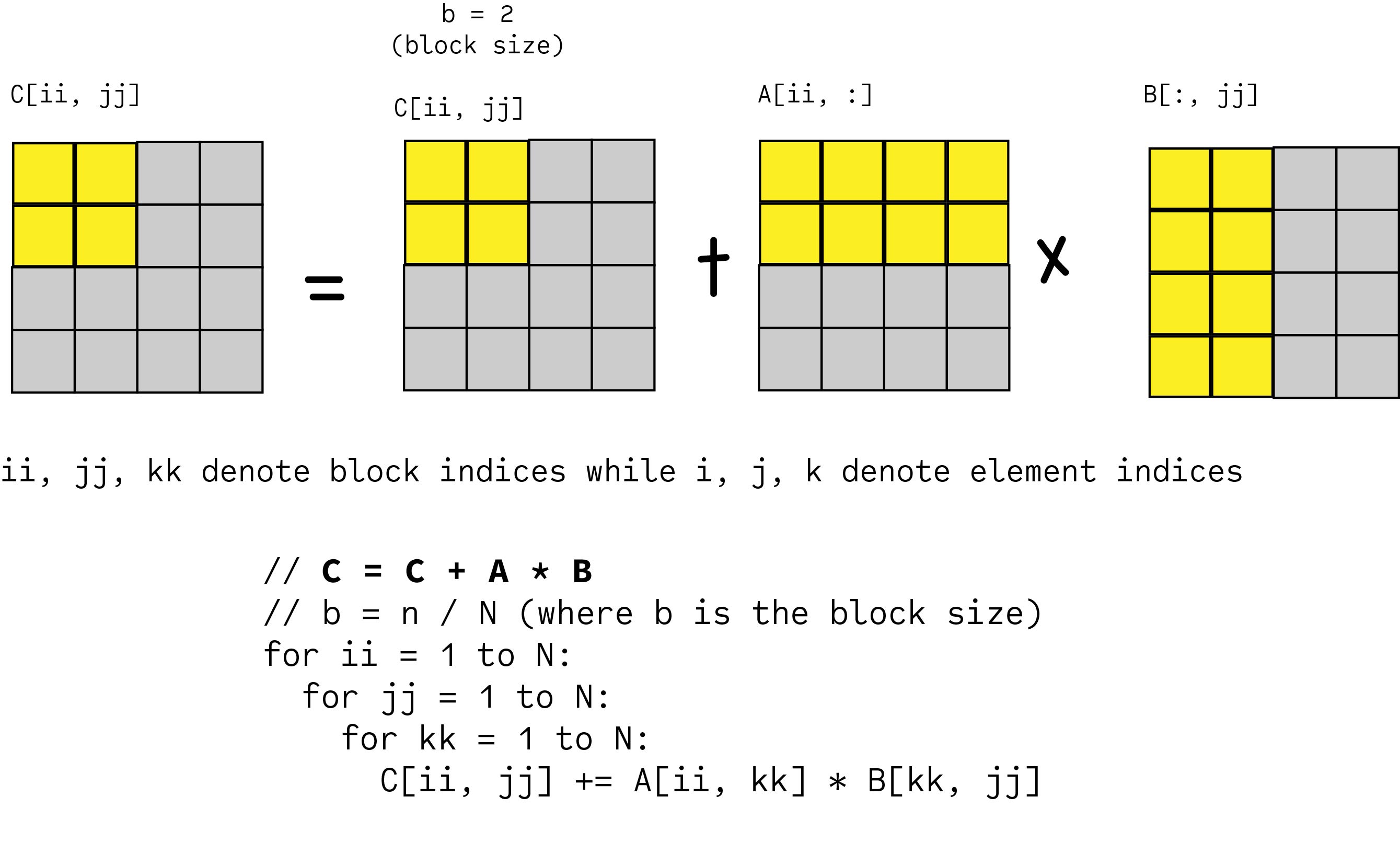
Blocked Matrix Multiplication Malith Jayaweera

Blocked Matrix Multiplication Malith Jayaweera

Matrix Multiplication Tiled Implementation Youtube

Fast Matrix Multiplication Cache Usage Ppt Download

Matrix Multiplication Tiled Implementation With Visible L1 Cache Youtube

Cache Lab Implementation And Blocking Ppt Video Online Download
Https Passlab Github Io Csce513 Notes Lecture10 Localitymm Pdf