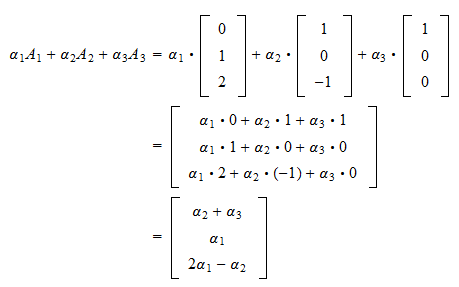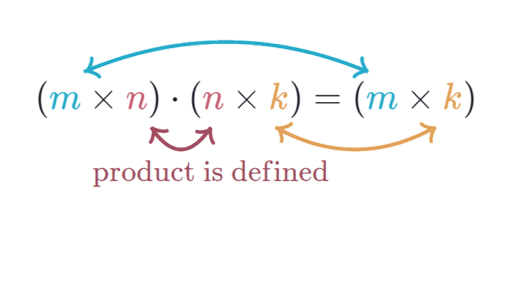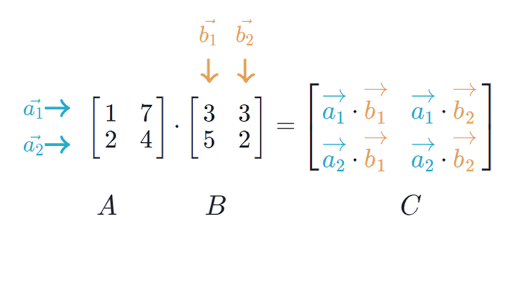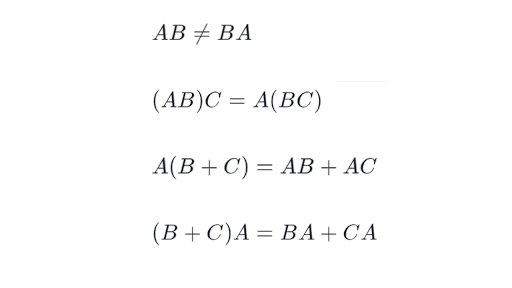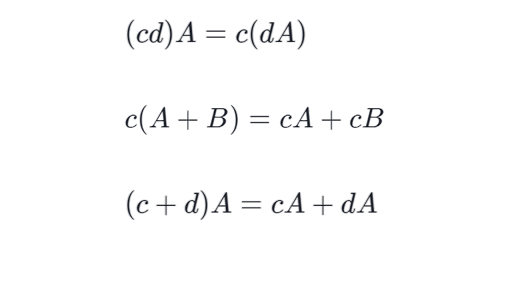Matrix Vector Calculation Rules
If you get stuck just consider each element of the matrix in isolation and apply the usual scalar derivative rules. The pushforward along a vector function f with respect to vector v in R n is given by d f v f v d v.
Ie AT ij A ji ij.

Matrix vector calculation rules. If p happened to be 1 then B would be an n 1 column vector and wed be back to the matrix-vector product The product A B is an m p matrix which well call C ie A B C. Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. In vector calculus the derivative of a vector function y with respect to a vector x whose components represent a space is known as the pushforward or differential or the Jacobian matrix.
In this book we will study two complementary questions about a matrix equation Ax b. If we let A x b then b is an m 1 column vector. A 3 m 3733 219 It still points in the same direction but is 3 times longer.
In mathematics a matrix plural matrices is a rectangular array or table of numbers symbols or expressions arranged in rows and columns. Rules for Vector Differentiation Vector differentiation follows similar rules to scalars regarding vector addition multiplication by a scalar and products. Reduce vector expressions down to a set of scalar expressions and then take all of the partials combining the results appropriately into vectors and matrices at the end.
We multiply rows by coloumns. The definition of the product of a matrix by a column was motivated by the notation for a system of m linear equations in n unknowns x 1 to xn. Multiply the vector m 73 by the scalar 3.
This means you take the first number in the first row of the second matrix and scale multiply it with the first coloumn in the first matrix. That is a generally useful trick. Now we can define the linear transformation.
You do this with each number in the row and coloumn then move to the next row and coloumn and do the same. See the answer See the answer See the answer done loading. Let A be an m n matrix let u v be vectors in R n and let c be a scalar.
In eqn5 xis a column vectorknown as n-by-1 matrix and the result f x ahas the same size. The vector addition is. Free matrix and vector calculator - solve matrix and vector operations step-by-step This website uses cookies to ensure you get the best experience.
In math terms we say we can multiply an m n matrix A by an n p matrix B. Displaystyle dmathbf f mathbf v frac partial mathbf f partial mathbf v dmathbf v. Matrix-vector product A Matrix and a vector can be multiplied only if the number of columns of the matrix and the the dimension of the vector have the same size.
Answer to Question 1 Vector and matrix calculation. VECTOR AND MATRIX ALGEBRA 433 824 6 Feb 2 A BX AX BX distributive laws AX Y AX AY. The numbering starts at the top left of the matrix and going from left to right and from top to bottom.
You can write AX R as an abbreviation for the system. Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. 1 8 This problem has been solved.
Axchspace30pxnormalsize c_ilargedisplaystyle sum_tiny ja_ijx_j. Later well show that with some matrix properties this formula can be derived without using f x as a bridge. A u v Au Av.
Provided that they have the same dimensions each matrix has the same number of rows and the same number of columns as the. Let us define the multiplication between a matrix A and a vector x in which the number of columns in A equals the number of rows in x. Matrix-vectorproduct very important special case of matrix multiplication.
If for a matrix is n m then the matrix is called a square matrix. F xT f xT aT 7 Note that we only use the organization de nition in this example. In particular we have that for any vectors A B and any scalar α dαA dαA αdA dA B dA dB.
By this de nition we have. For example the dimension of the matrix below is 2 3 read two by three because there are two rows and three columns. So if A is an m n matrix then the product A x is defined for n 1 column vectors x.
Y Ax A is an mn matrix x is an n-vector y is an m-vector y i A i1x1A inx n i 1m can think of y Ax as a function that transforms n-vectors into m-vectors a set of m linear equations relating x to y Matrix Operations 29. The first index is the row number and the second index is the column number. A matrix equation is an equation of the form Ax b where A is an m n matrix b is a vector in R m and x is a vector whose coefficients x 1 x 2 x n are unknown.
The multiplication of a vector by a scalar positive λ only changes the length. And now you know why numbers are called scalars because they scale the vector up or down. By using this website you agree to our Cookie Policy.
Calculation rules for vectors Multiplication of a vector with a scalar. Vectors are added component by component in Cartesian coordinates.
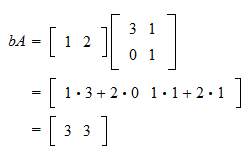
Matrix Multiplication And Linear Combinations
Matrix Multiplication Dimensions Article Khan Academy
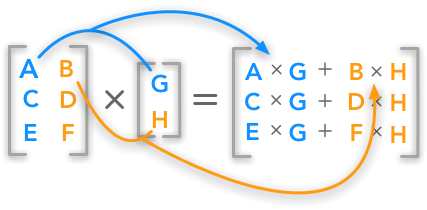
Introduction To Matrices And Vectors Multiplication Using Python Numpy
Multiplying Matrices Article Matrices Khan Academy

Why Does Matrix Multiplication Work The Way It Does By Erik Engheim Medium
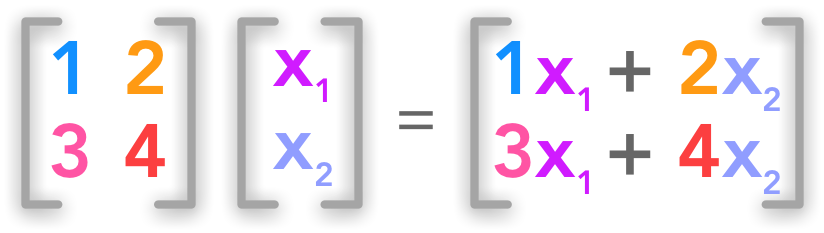
Introduction To Matrices And Vectors Multiplication Using Python Numpy
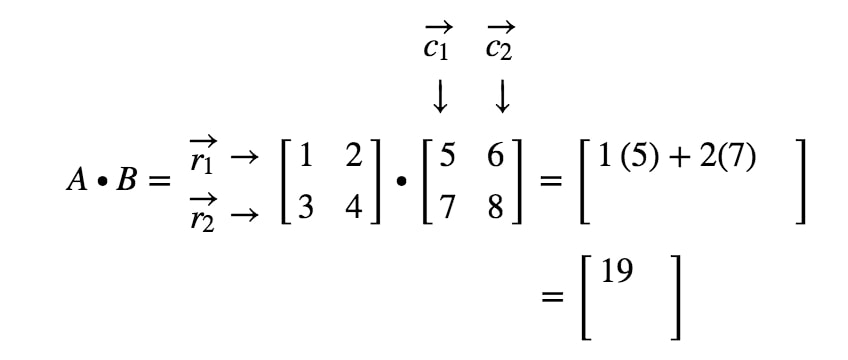
How To Multiply Two Matrices Together Studypug
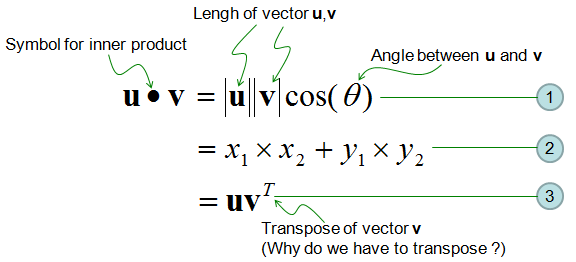
Vector Inner Product Sharetechnote

7 1 Matrices Vectors Addition And Scalar Multiplication Ppt Download
Properties Of Matrix Multiplication Article Khan Academy
Properties Of Matrix Scalar Multiplication Article Khan Academy
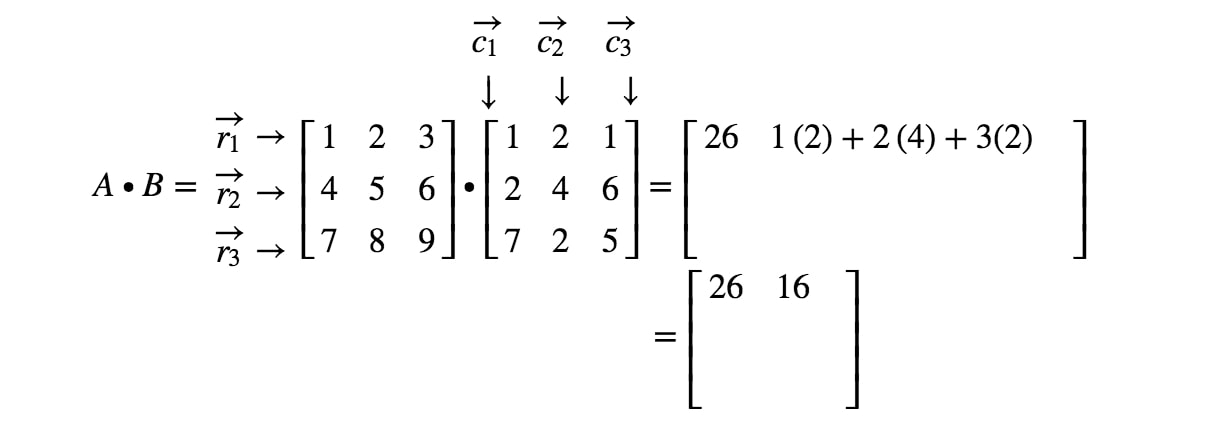
How To Multiply Two Matrices Together Studypug

Difference Between A Row Column Vector Video Lesson Transcript Study Com
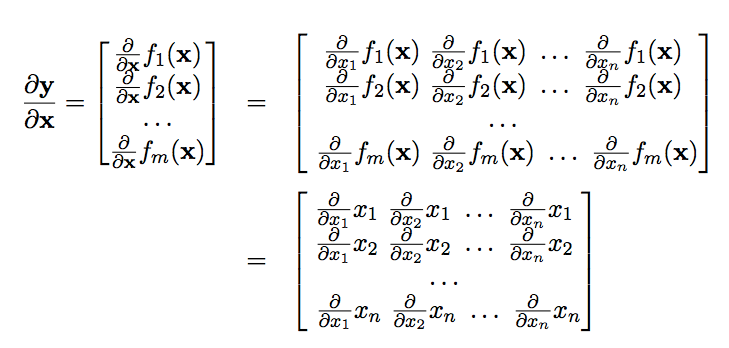
Finding The Gradient Of A Vector Function By Chi Feng Wang Towards Data Science
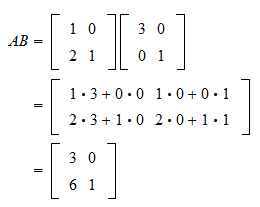
Matrix Multiplication And Linear Combinations
Matrices Algebra All Content Math Khan Academy

7 1 Matrices Vectors Addition And Scalar Multiplication