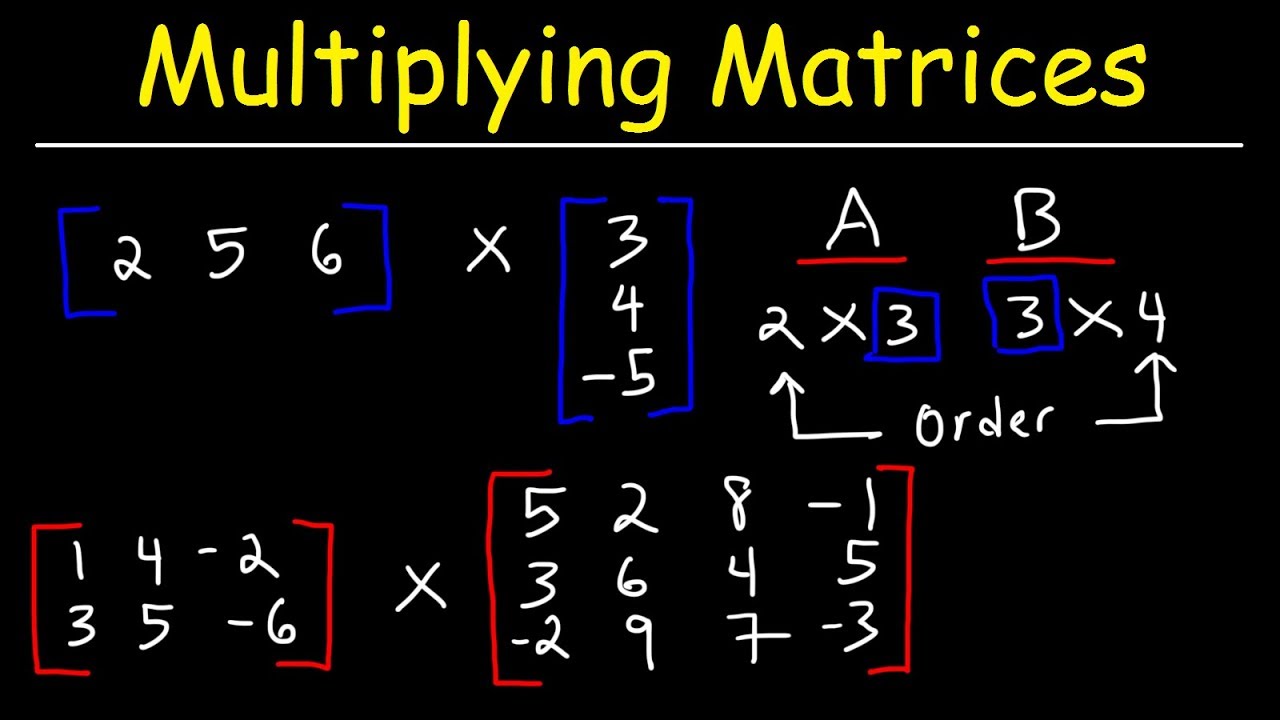
Multiplying Blocks Of Matrices
If fast memory has size M fast 3b 2 M fast q b M fast 3 12. Algebra is best done with block matrices.
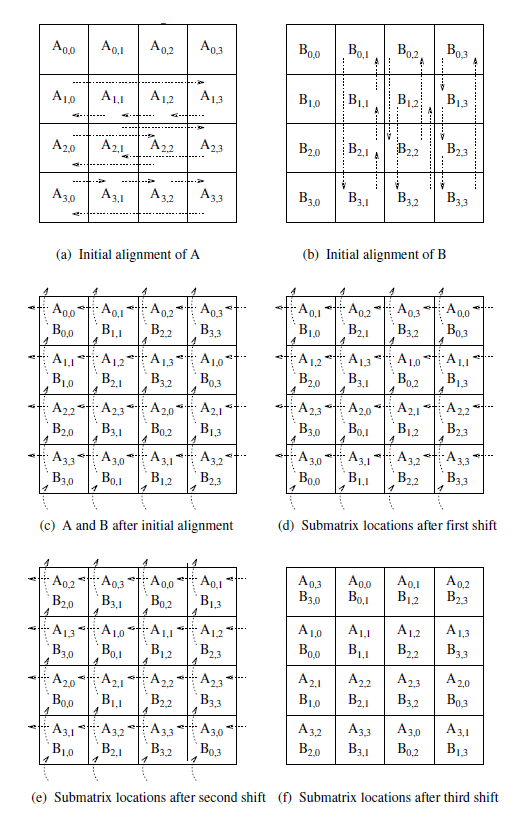
Cannon S Algorithm For Distributed Matrix Multiplication
An ordered partition my term is a set of ordered subsets J J 1J 2J p which come.
Multiplying blocks of matrices. Suppose n 12n is the ordered sequence of integers from 1 to n. Then the blocks are stored in auxiliary memory and their products are computed one by one. In the previous example M 1 1 0 1N 1 0 1 1.
What this means is that multiplying a row by b a is replaced B A 1 or A 1 B depending on the particular case. Block Multiplication of Matrices This note describes multiplication of block partitioned matrices. So you could also repeat the above tests by splitting up the two matrices in bigMatrix into 5 5 blocks for example.
The MATLAB equivalent is the operator. However it is also useful in computing products of matrices in a computer with limited memory capacity. The matrices are partitioned into blocks in such a way that each product of blocks can be handled.
6 NM 1 1 1 2. Multiplication of block matrices. Multiplying two matrices represents applying one transformation after anotherHelp fund future projects.
In particular exible thinking about the process of matrix multiplication can reveal concise proofs of important theorems and expose new results. Now you have a comprehensive understanding of blocked matrix multiplication. Listen to my latest Novel narrated by me.
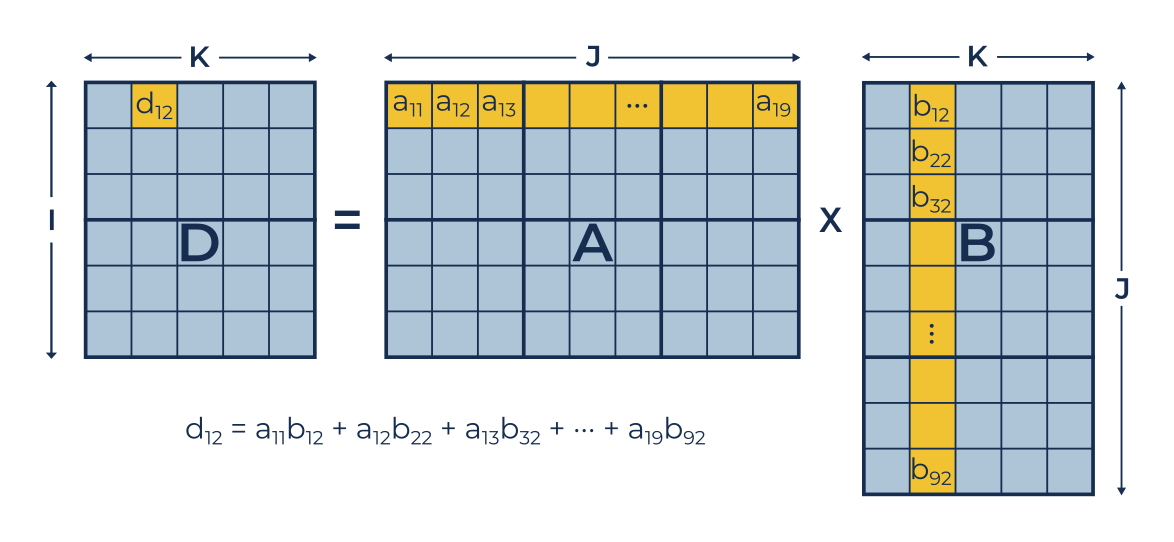
It is sometimes convenient to work with matrices split in blocks. The function blockMultiply is intended to work for any number of arguments in a matrix multiplication and also for any dimension as long as all adjacent factor share a common dimension as required by Dot. In a previous post I discussed the general problem of multiplying block matrices ie matrices partitioned into multiple submatrices.
So far I am doing this operation using npdot. TrMN trX l Mi l N l j X i X l Mi l N l i X l X i Nl iM i l trX i Nl iM i l trNM. Block multiplication has theoretical uses as we shall see.
When the value of the Multiplication parameter is Matrix the Product block is in Matrix mode in which it processes nonscalar inputs as matrices. Do you have recommendations how to speed it up using either npeinsum or to exploit the block diagonality of matrix a. Viewing linear algebra from a block-matrix perspective gives an instructor access.
A special case gives a representation of a matrix as a sum of rank one matrices. While matrix multiplication does not commute the trace of a product of matrices does not depend on the order of multiplication. 15 hours agoand want to compute npdotan where n is a covariance matrix that has entries everywhere symmetric and positive definite.
We have already used this when we wrote Mv 1vnMv 1Mvn More generally if we have two matrices M P with dimensions that allow for multiplication ie. In Matrix mode the Product block can invert a single square matrix or multiply and divide any number of matrices that have dimensions for which the result is mathematically defined. However we cannot make the matrix sizes arbitrarily large because all three blocks have to fit inside the memory.
MN 2 1 1 1. Then you simply eliminate row and column entries just as you would do with two by two case. This also came up in exercise 1424 as well which I answered without necessarily fully understanding the problem.
To get half of the machine peak capacity q t m t f Therefore to run blocked matrix multiplication at half of the peak machine capacity 3q 2 3b 2. Gauss Elimination method also works in block matrix form provided that fractions are replaced with the nonsingular matrices properly. A A 11 A.
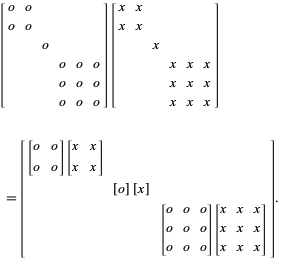
Multiplying block matrices. Suppose A is a 2 2 block matrix say having I J rows and K L columns so that the block in the upper left corner is I K etc. In doing exercise 1610 in Linear Algebra and Its Applications I was reminded of the general issue of multiplying block matrices including diagonal block matrices.
Then when B is a 2 2 block matrix having K L rows and M N columns the block multiplication A B would be compatible. I then discussed block diagonal matrices ie block matrices in which the off-diagonal submatrices are zero and in a multipart series of posts showed that we can uniquely and maximally partition any square matrix into block. The number of columns of M equals the number of.
Thus trMN trNM for any square matrices Mand N. If one partitions matrices C A and Binto blocks and one makes sure the dimensions match up then blocked matrix-matrix multiplication proceeds exactly as does a regular matrix-matrix multiplication except that individual multiplications of scalars commute while in general individual multiplications with matrix blocks submatrices do not.
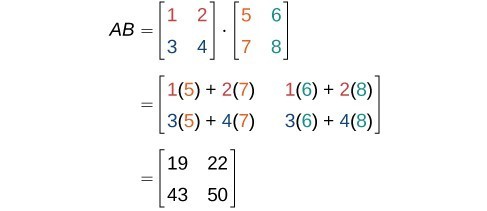
Finding The Product Of Two Matrices College Algebra
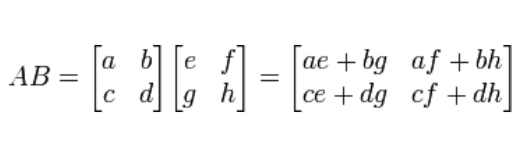
Breakthrough Faster Matrix Multiply
Matrix Matrix Multiplication Ml Wiki
Https Passlab Github Io Csce513 Notes Lecture10 Localitymm Pdf
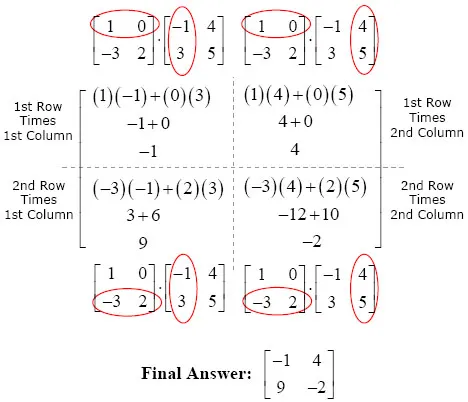
Matrix Multiplication Made Easy In Java

Tiled Algorithm An Overview Sciencedirect Topics

Java Program To Multiply 2 Matrices Javatpoint
Matrix Multiplication From Wolfram Mathworld

Lecture 4 Matrix Operations And Elementary Matrices Youtube

Matrix Processing With Nanophotonics By Martin Forsythe Lightmatter Medium
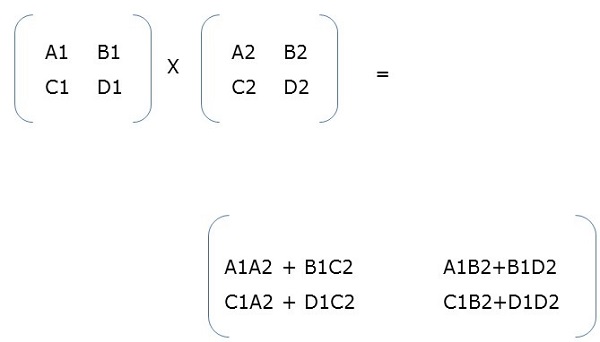
Parallel Algorithm Matrix Multiplication Tutorialspoint
Matrix Processing With Nanophotonics By Martin Forsythe Lightmatter Medium

Multiplying Matrices Video Khan Academy
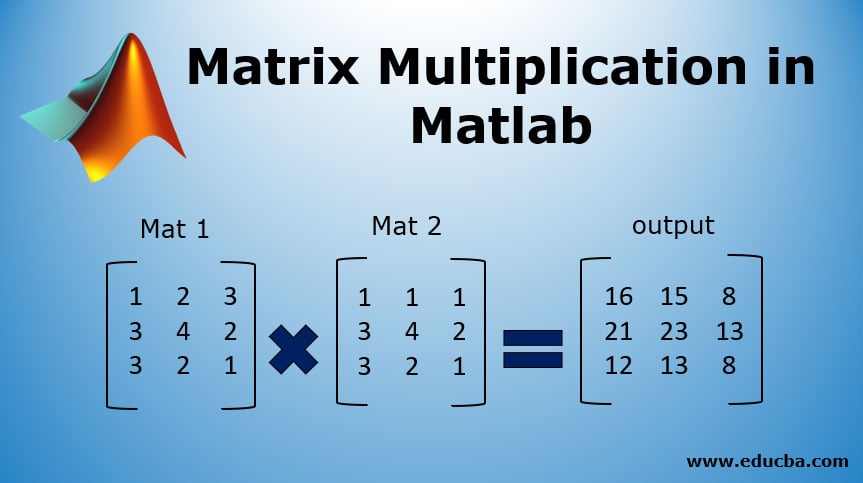
Matrix Multiplication In Matlab How To Perform Matrix Multiplication

Understanding Matrix Multiplication On A Weight Stationary Systolic Architecture Telesens
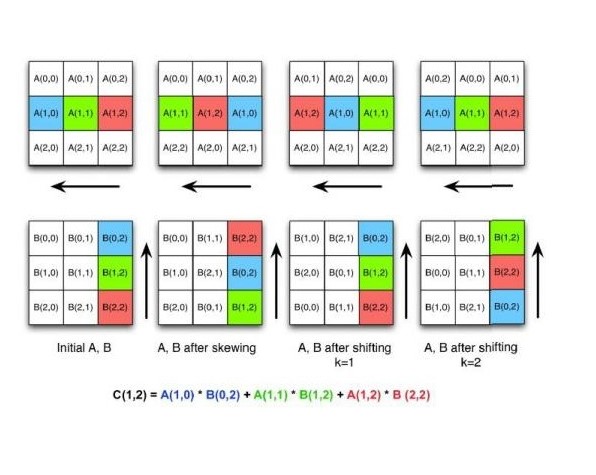
Cannon S Algorithm For Distributed Matrix Multiplication
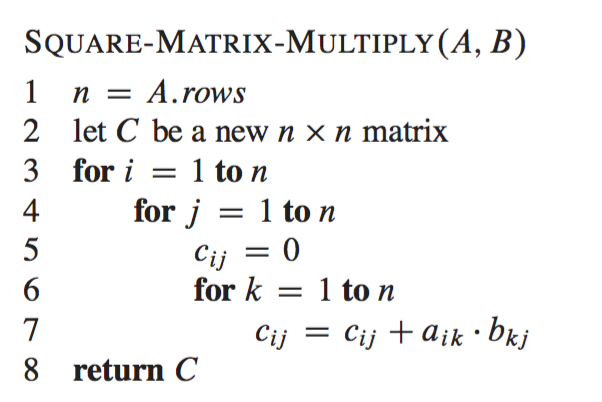
Matrix Multiplication Using The Divide And Conquer Paradigm

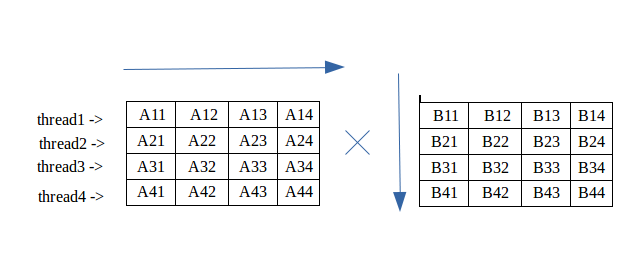
Multiplication Of Matrix Using Threads Geeksforgeeks