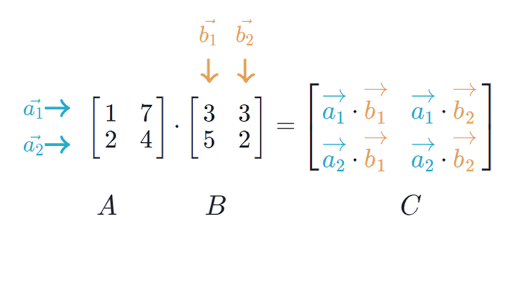The Fastest Matrix Multiplication Algorithm
Similarly to the analysis of Strassens algorithm. We implement a fast matrix multiplication algorithm withasymptotic complexityON2775 for squareNNmatrices dis-covered by Smirnov.

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange
The cur-rently fastest matrix multiplication algorithm with a complexity of On238 was obtained by Coppersmith and Winograd 1990.
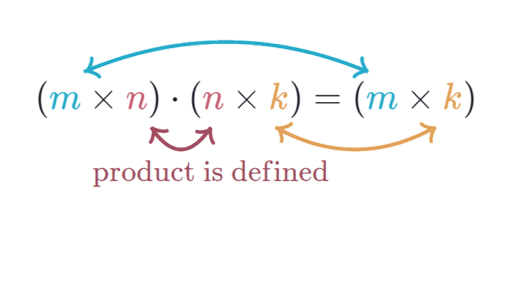
The fastest matrix multiplication algorithm. More information on the fascinat-. Fast Sparse Matrix Multiplication 3 1969 was the first to show that the naıve algorithm is not optimal giving an On281 algorithm for the problem. As of April 2014 the asymptotically fastest algorithm runs in O n 23728639 time.
Example of Matrix multiplication. The first to be discovered was Strassens algorithm devised by Volker Strassen in 1969 and often referred to as fast matrix multiplication. Fast and stable matrix multiplication p1344.
Group-theoretic algorithms for matrix multiplication FOCS Proceedings 2005. Volker Strassen surprised the community by publishing an algorithm that multiplies a 22 matrix in 7 multiplications rather than 8 10. Found groups with subsets beating the sum of the cubes and satisfying the triple product property.
Francois LeGall Powers of Tensors and Fast Matrix Multiplication 30 Jan 2014. There are many different implementation. However our performance results show that thisalgorithm is not practical for the problem sizes that we consider.
At the time multiplications were very expensive operations compared to subtractions and additions and so the number of multiplications was. It is based on a way of multiplying two 2 2 -matrices which requires only 7 multiplications instead of the usual 8 at the expense of several additional addition and subtraction operations. Century the algorithms that we know as Gauss-Jordan Elimination and matrix multiplication were assumed to be optimal.
Many improvements then followed. The algorithm above gives the following recursive equation Nn3Nn12 1On and N27. Altogether Strassens algorithm improved the speed of matrix multiplication from n3 to n281 multiplicative steps.
Strassens algo-rithm is an improvement over the naive algorithm in the case of multiplying two 22 matrices because it. The slow matrix multiplication algorithm runs in time O n 3 and uses O n 2 memory. An interesting new group theoretic approach to the matrix.
More information on the fascinating subject of matrix multiplication algorithms and its history can be found in Pan Pan85 and Burgisser et al. The currently fastest matrix multiplication algorithm with a complexity of On238 was obtained by Coppersmith and Winograd CW90. The fastest matrix multiplication runs in time n ω o 1 where ω is the linear algebra constant but what is known about its memory complexity.
Fast matrix multiplication is still an open problem but implementation of existing algorithms 5 is a more com-mon area of development than the design of new algorithms 6. As It can multiply two n n matrices in 0n2375477 time. In terms of asymptotic complexitythis is the fastest matrix multiplication algorithm implementa-tion to date.
SIAM News Nov 2005 by Sara Robinson. The next big improvement took place in the late 1970s with a fundamentally new way to approach the problem. Nn denote the number of arithmetic operations that the above algorithm needs to multiply polynomial of degree n.
Many improvements then followed. It seems that it may be possible a priori that fast matrix multiplication consumes n ω memory. BLAS is the best ready-to-use efficient matrix multiplication library.
Here is a benchmark I made for some implementations on a MacBook Pro with dual-core Intel Core 2 Duo 266 GHz. The fastest matrix multiplication algorithm The matrix multiplication concept is vastly used in scientific computing computer graphics and pattern recognition fields. But the algorithm is not very practical so I recommend either naive multiplication which runs in O n 3 or Strassens algorithm which runs in O n 28.
Recently I have learned about both the Strassen algorithm and the CoppersmithWinograd algorithm independently according to the material Ive used the latter is the asymptotically fastest known matrix multiplication algorithm until 2010.

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
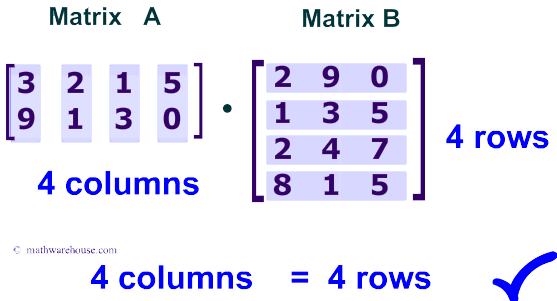
Matrix Multiplication Dimensions Article Khan Academy

Figure 1 1 Input Array Extracted From The Bank S Database Algorithm Matrix Multiplication Math Tricks
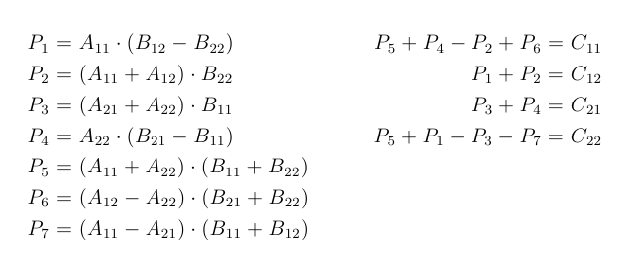
Strassen Matrix Multiplication C The Startup
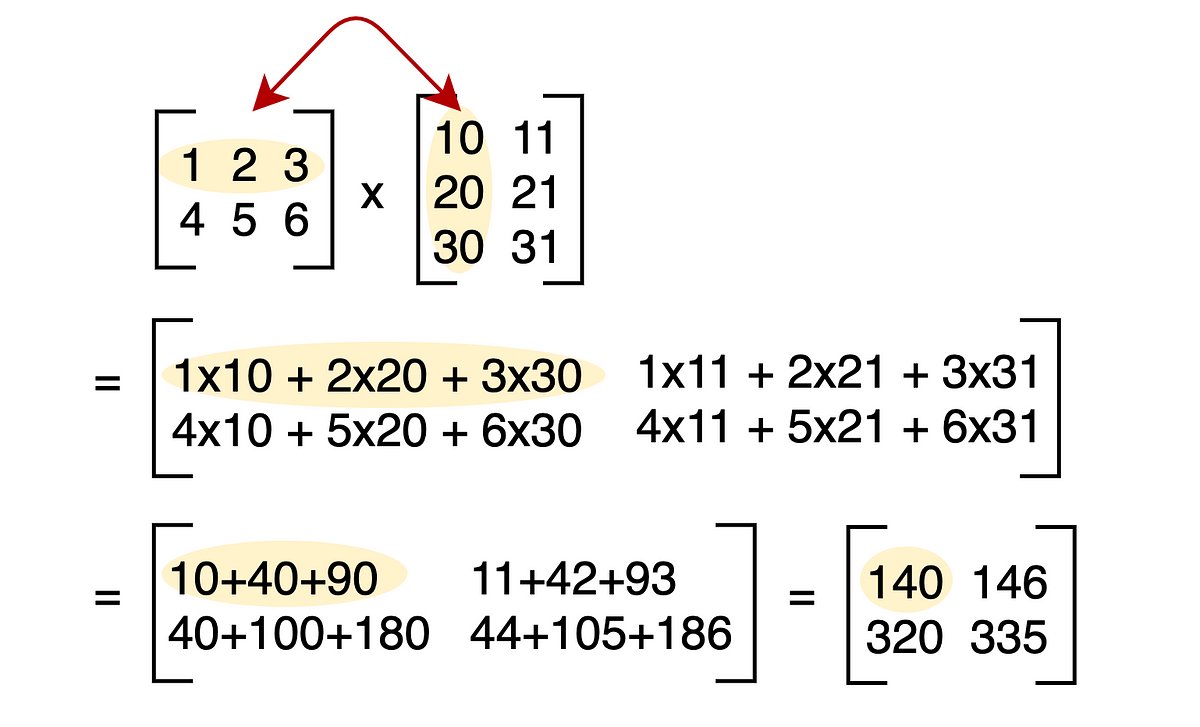
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Proposed 4 4 Matrix Multiplication Method A Partitioning Of A 4 Download Scientific Diagram

Sparse Matrix Multiplication Description By Glyn Liu Medium

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Matrix Multiplication Calculator

2 9 Strassens Matrix Multiplication Youtube

Pseudocode For Matrix Multiplication Download Scientific Diagram

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Matrix Multiplication Data Science Pinterest Multiplication Matrix Multiplication And Science

Matrix Multiplication With 1 Mapreduce Step Geeksforgeeks
Matrix Multiplication In C Applying Transformations To Images Codeproject
Multiplying Matrices Article Matrices Khan Academy
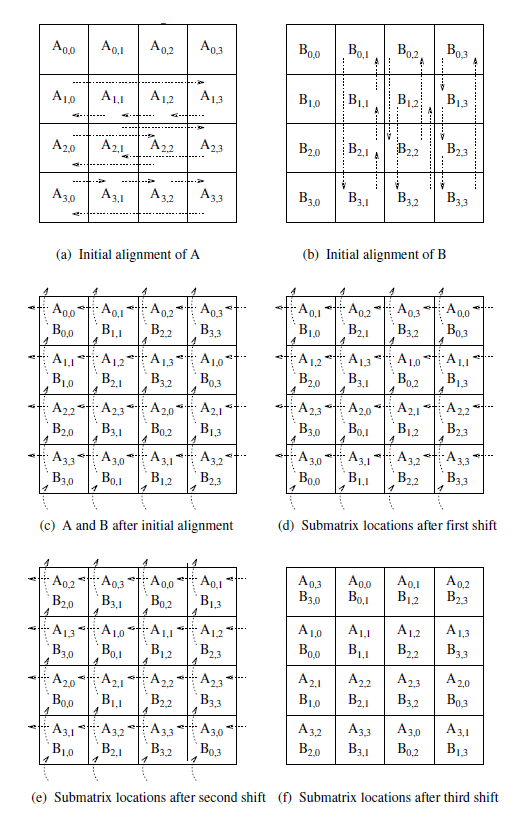
Cannon S Algorithm For Distributed Matrix Multiplication