What Is The Time Complexity Of The Fastest Known Matrix Multiplication Algorithm
Recently I have learned about both the Strassen algorithm and the CoppersmithWinograd algorithm independently according to the material Ive used the latter is the asymptotically fastest known matrix multiplication algorithm until 2010. As It can multiply two n n matrices in 0 n2375477 time.

Strassen S Matrix Multiplication
Mn V-1 D V V-1 D V.

What is the time complexity of the fastest known matrix multiplication algorithm. Often these are written in big-O notation where an algorithm running in time means that there is some constant for which the runtime will never exceed for an input of length. The Karatsuba algorithm is a fast multiplication algorithm. If all three matrices were square then the fastest known algorithm for multiplying two of them has complexity O N 23729.
Because of the overhead of recursion Karatsubas multiplication is slower than long multiplication for small values of n. You can do that in logarithmic time in n. Since The Coppersmith-Winograd algorithm multiplies the matrices in O n 237 time.
According to the Wikipedia article Fürers algorithm it has been conjectured that the asymptotically fastest multiplication algorithm runs in time O n log. It reduces the multiplication of two n-digit numbers to at most n log 2 3 n 158 displaystyle nlog _23approx n158 single-digit multiplications in general. Because all the V and V-1 terms cancel.
This means that multiplying three N N matrices will have complexity just under O N 475. Francois LeGall Powers of Tensors and Fast Matrix Multiplication 30 Jan 2014. For example the Karatsuba algorithm.
The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of O n 23737. It seems that it may be possible a priori that fast matrix multiplication consumes n ω memory. Opened on Nov 18 2019.
Solvay Strassen algorithm achieves a complexity of O n 2807 by reducing the number of multiplications required for each 2x2 sub-matrix from 8 to 7. Karatsuba multiplication has a time complexity of On log 2 3 On 1585 making this method significantly faster than long multiplication. It was discovered by Anatoly Karatsuba in 1960 and published in 1962.
V-1 D V V-1 Dn V. The fastest matrix multiplication runs in time n ω o 1 where ω is the linear algebra constant but what is known about its memory complexity. As of April 2014 the asymptotically fastest algorithm runs in O n 23728639 time.
Each step of getting the next x t can be done in the time of which ever is more of the multiplication algorithm or division by t. The slow matrix multiplication algorithm runs in time O n 3 and uses O n 2 memory. But the algorithm is not very practical so I recommend either naive multiplication which runs in O n 3 or Strassens algorithm which runs in O n 28.
The time complexity of recursive multiplication of two square matrices by Strassens Method is found to be O n 280. In the case of matrix multiplication the best-known algorithm runs in polynomial. Since D is diagonal you just have to raise a bunch of real numbers to the nth power rather than full matrices.
Typical implementations therefore switch to long multiplication for small values of n. Other algorithms which are faster than Grade School Multiplication algorithm are Karatsuba multiplication which has a time complexity of O n log 2 3 O n 1585 and Toom 3 algorithm which has a time complexity of Θ n 1465 Note that these are the fast algorithms. It is therefore asymptotically faster than the traditional algorithm which requires n 2 displaystyle n2 single-digit products.
The computational complexity class of an algorithm is a measure of how the runtime increases as the input becomes larger.
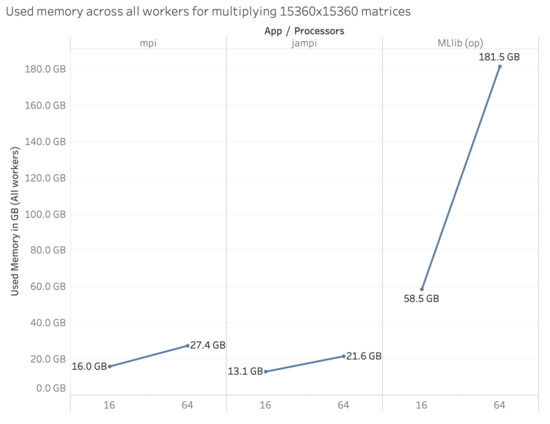
Bdcc Free Full Text Jampi Efficient Matrix Multiplication In Spark Using Barrier Execution Mode Html

The Weight And Sum Operation For A Neural Network Is A Dot Product The Walsh Hadamard Transform Is A Collection Of Dot Pro Words Word Search Puzzle Networking

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Matrix Multiplication Algorithm Wikiwand
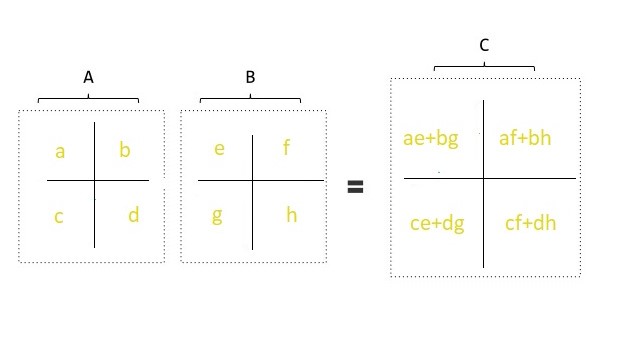
Strassen S Matrix Multiplication Algorithm

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Dijkstra Complexity Analysis Dijkstra S Algorithm Algorithm Graphing

Hpmax Heterogeneous Parallel Matrix Multiplication Using Cpus And Gpus Springerlink
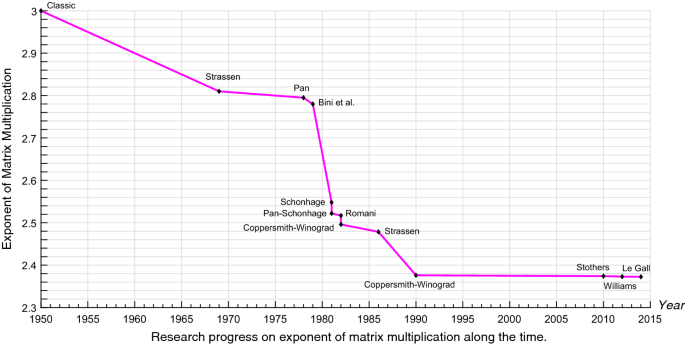
An Introduction To The Computational Complexity Of Matrix Multiplication Springerlink




