Symmetric Matrix Is Nonsingular

02 Jun, 2021

Prove That I -S Is Nonsingular. They are all singular that is determinant is zero Since others have already shown that not all symmetric matrices are invertible I will add when a symmetric matrix.

Check If A Matrix Is Invertible Geeksforgeeks

A Show that if and are nonsingular matrices then the product is also nonsingular.

Symmetric matrix is nonsingular. 1728k 1733k 328. The result we have just proved in the previous problem is relevant. Prove that the inverse of a symmetric nonsingular matrix is symmetric.

It follows that is positive definite if and only if both and are positive definite. Now we need to examine the transpose of A1. Prove That ---------.

If A and B are non-singular matrices of the same order then AB is non-singularIf A is non-singular then Ak is non-singular for any positive integer k. If is a square matrix such that then write whether is symmetric or skew-symmetric. Since A is nonsingular A1 exists.

Show that if A is a symmetric nonsingular matrix then A1 is also symmetric. To prove that the inverse of A is symmetric you need to show that A 1 T A 1. B Show that if is nonsingular then the column vectors of are linearly independent.

Jimin He Zhi-Fang Fu in Modal Analysis 2001. I Let A be a symmetric nonsingular matrix. Which shows that is congruent to a block diagonal matrix which is positive definite when its diagonal blocks are.

A canonical form of with respect to congruence transformations was given by Sergeichuk 1988 up to classification of symmetric and Hermitian forms over finite extensions of. Otherwise is called singular. In the latter case A is also nonsingular.

So a non symmetric matrix is one which when transposed gives a different matrix than the one you started with. Since A is symmetric AT A. If A is a skew-symmetric matrix which is also a square matrix then the determinant of A should satisfy the below condition.

Iii Use the properties of. Properties of non-singular matrix. 114k 2291k 513.

Consider The Block Matrix M Rex Bxs Suppose That Both A And SB-RA-C Are Nonsingular. Let be a field of characteristic not and let be a pair of matrices over in which is symmetric and is skew-symmetric. The rank of a matrix A is equal to the order of the largest non-singular submatrix of AIt follows that a non-singular square matrix of n n has a rank of nThus a non-singular matrix is also known as a full rank matrix.

Often appear in applications. Ii This means that A T A and A 1 exists. All of the eigenvalues of a variance-covariance matrix.

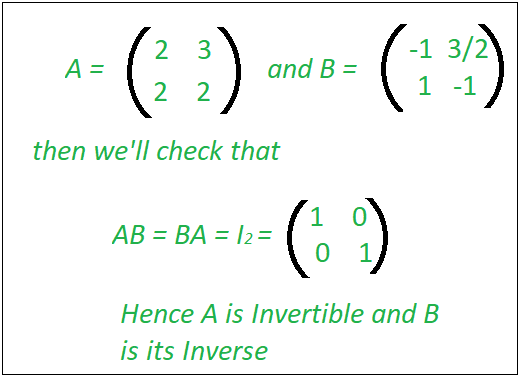
An n x n square matrix A is called non-singular if there exists an n x n matrix B such that AB BA In where In denotes the n x n identity matrix. Det A T det -A -1 n detA. This video explains the concept of a Symmetric Matrix.

214 The rank of a matrix. The following is a ready consequence. We can use this observation to prove that A T A is invertible because from the fact that the n columns of A are linear independent we can prove that A T A is not only symmetric but also positive definite.

Let S Be A Skew-symmetric Matrix With Real Entries. Determinant of Skew Symmetric Matrix. If A is a symmetric and B skew symmetric matrix and is non-singular and then prove that.

An matrix is called nonsingular if the only solution of the equation is the zero vector. For example I want to create a 33 non-singular symmetric matrix using randomly generated real numbers number_list ab. If A is non-singular and k is a non-zero scalar then kA is.

And the list goes on. A symmetric matrix A is positive semideﬁnite if and only if all of its eigenvalues are 0. Consider given by and.

A sufficient condition for a symmetric n n matrix C to be invertible is that the matrix is positive definite ie. If A I S1-5-1 Show That A-1 AT. If the matrix is non-singular then its inverse exists.

Symmetric block matrices. This video explains what Singular Matrix and Non-Singular Matrix are. X R n 0 x T C x 0.

To learn more about Matrices enroll in our full course now. A is positive deﬁnite if and only if all of its eigenvalues are 0. To learn more about Matrices enroll in our full course now.

It is incorrect the 0 matrix is symmetric but not invertable. For Matrices Such That The Product AB Is Defined Explain Why. We obtain a simpler canonical form of if is nonsingular.

The determinant of skew symmetric matrix is non-negative. When identity matrix is added to skew symmetric matrix then the resultant matrix is invertible. I want to create a non-singular symmetric matrix using random real numbers.

A non-singular matrix is a square one whose determinant is not zero. A symmetric matrix is a matrix which does not change when transposed. If is nonsingular then we can write.

The identity matrix is symmetric whereas if you add just one more 1 to any one of its non diagonal elements then it becomes non symmetric. A1T AT1 by previous problem A1 since AT A.

Symmetric Matrix An Overview Sciencedirect Topics